Cho hình chóp tứ giác đều (S.ABCD) có cạnh đáy bằng a (a > 0). Các điểm M, N, P lần lượt là trung điểm của SA, SB, SC. Mặt phẳng (MNP) cắt hình chóp theo một thiết diện có diện tích bằng:

I. Vị trí tương đối của hai đường thẳng trong không gian.

Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:

- Trường hợp 1. Có một mặt phẳng chứa a và b.

Khi đó, ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có 3 khả năng xảy ra:

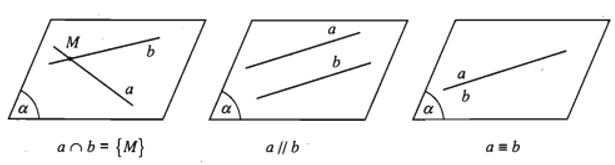
i) a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu $a\cap b=\left\{M\right\}$. Ta có thể viết $a\cap b=M$.

ii) a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.

iii) a trùng b, kí hiệu là $a\equiv b$.

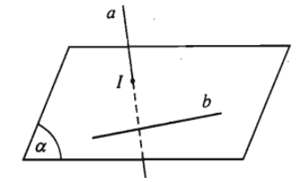
- Trường hợp 2. Không có mặt phẳng nào chứa a và b.

Khi đó ta nói a và b chéo nhau hay a chéo với b.

- Ví dụ 1. Cho tứ diện ABCD. Hãy chỉ ra các cặp đường thẳng chéo nhau.

Lời giải:

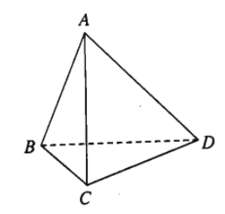
Đường thẳng AB và CD chéo nhau.

Đường thẳng AC và BD chéo nhau.

Đường thẳng AD và BC chéo nhau.

II. Tính chất

- Định lí. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

- Định lí (về giao tuyến của ba mặt phẳng).

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

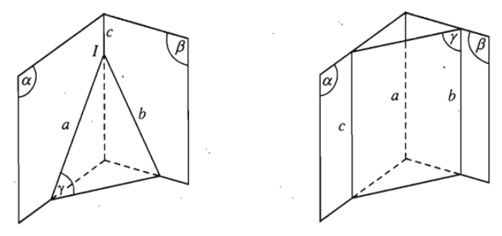
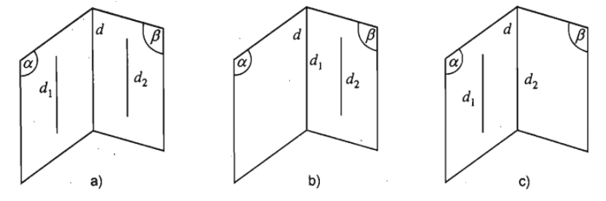
- Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:

a) (SAD) và (SBC).

b) (MCD) và (SAB), với M là một điểm bất kì thuộc cạnh SA.

Lời giải:

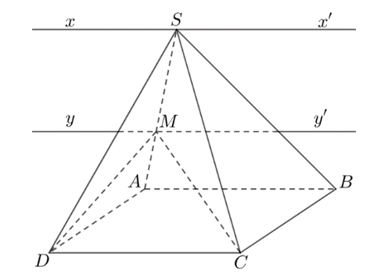
a) Ta có: $\left\{\begin{array}{l}S\in \left(SAB\right)\cap \left(SCD\right)\\ AB\subset \left(SAB\right)\\ CD\subset \left(SCD\right)\\ AB\text{//}CD\end{array}\right.$.

$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=Sx$, với  Sx // AB // CD.

b) Ta có: $\left\{\begin{array}{l}M\in \left(SAB\right)\cap \left(MCD\right)\\ AB\subset \left(SAB\right)\\ CD\subset \left(MCD\right)\\ AB\text{//}CD\end{array}\right.$.

$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=My$, với My // AB // CD.

- Định lí. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

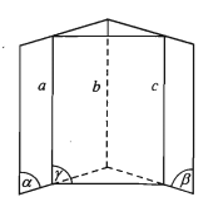
Ta có: a // c; b // c nên a // b hay a // b // c (ba đường thẳng song song).

 Ví dụ 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng IJ // AB, từ đó suy ra IJ // CD.

Lời giải:

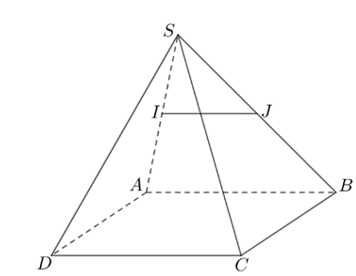
Xét tam giác SAB có I, J lần lượt là trung điểm của các cạnh SA, SB nên IJ là đường trung bình của tam giác SAB.

Từ đó suy ra IJ // AB.

Lại có AB // CD (vì ABCD là hình bình hành) nên từ đó ta có IJ // CD (vì cùng song song với đường thẳng AB).