Chứng minh rằng phương trình sau có ít nhất hai nghiệm:
 Giải bởi Vietjack
Giải bởi Vietjack
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
- Xét hàm số: là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
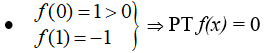
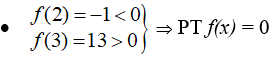
- Mà nên PT f(x) = 0 có ít nhất 2 nghiệm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, . Tính góc giữa SC và mp (SAB).
Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng:
Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với
Cho hình lập phương . Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, . Chứng minh rằng: (SAC) ⊥ (SBD).
Phần I: Trắc nghiệm
Cho hàm số có đồ thị (C) . Khi đó tiếp tuyến của (C) tại điểm M( 1; 2003) có hệ số góc là:
Cho cấp số nhân lùi vô hạn có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây:
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm ?