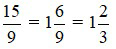Tìm dấu thích hợp (>, <) thay cho dấu "?".
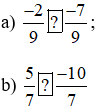
 Giải bởi Vietjack
Giải bởi Vietjack
a) Hai phân số đã cho có chung mẫu nên ta chỉ cần so sánh tử số với nhau:
Vì 2 < 7 nên -2 > - 7
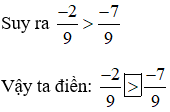
b) Hai phân số này có chung mẫu nên để so sánh thì ta chỉ cần so sánh tử số với nhau:
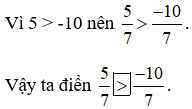
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
a) Viết phân số dưới dạng hỗn số;
b) Viết hỗn số dưới dạng phân số.
Em thực hiện các yêu cầu sau để quy đồng mẫu hai phân số và
- Tìm bội chung nhỏ nhất của hai mẫu số.
- Viết hai phân số mới bằng hai phân số đã cho và có mẫu là số vừa tìm được.
Bảng sau cho biết chiều dài (theo đơn vị feet, 1 feet xấp xỉ bằng 30,48 cm) của một số loài động vật có vú nhỏ nhất trên thế giới.
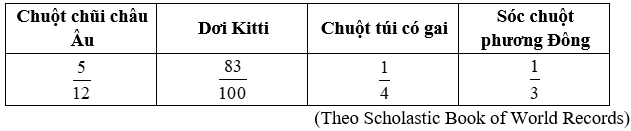
Hãy sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé.
a) Khối lượng nào lớn hơn: kg hay kg?
b) Vận tốc nào nhỏ hơn: km/h hay km/h?
Lớp 6A có 4/5 số học sinh thích bóng bàn, 7/10 số học sinh thích bóng đá và 1/2 số học sinh thích bóng chuyền. Hỏi môn thể thao nào được các bạn học sinh lớp 6A yêu thích nhất?

Tròn nói mỗi bạn được 1 cái bánh và cái bánh. Em có đồng ý với Tròn không?
Tình huống mở đầu:

Đề giải quyết tình huống mở đầu, ta cần so sánh và . Em hãy thực hiện các yêu cầu sau:
- Viết hai phân số trên dưới dạng hai phân số có cùng một mẫu dương bằng cách quy đồng mẫu số.
- So sánh hai phân số cùng mẫu vừa nhận được. Từ đó kết luận về phần bánh còn lại của hai bạn Vuông và Tròn.
Em hãy nhắc lại quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương), rồi so sánh hai phân số và
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số 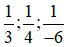 ta làm như sau:
ta làm như sau:
+ Đưa về các phân số có mẫu dương: 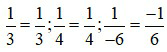 .
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
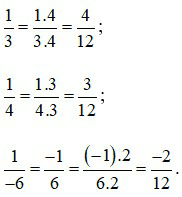
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: 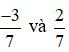 là hai phân số có cùng mẫu số dương.
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên 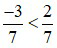 .
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: 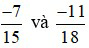 .
.
BCNN (15; 18) = 90
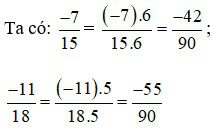
Vì –42 > –55 nên  do đó,
do đó,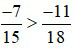
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi 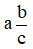 là một hỗn số dương với a là phần nguyên và
là một hỗn số dương với a là phần nguyên và  là phần phân số.
là phần phân số.
Ví dụ 4:
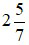 là một hỗn số dương với phần nguyên là 2 và phần phân số là
là một hỗn số dương với phần nguyên là 2 và phần phân số là 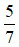 . Khi đó ta đọc
. Khi đó ta đọc 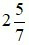 là hai năm phần bảy.
là hai năm phần bảy.
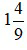 là một hỗn số dương với phần nguyên là 1 và phần phân số là
là một hỗn số dương với phần nguyên là 1 và phần phân số là 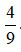 . Khi đó ta đọc
. Khi đó ta đọc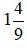 là một bốn phần chín.
là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số 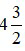 sang phân số:
sang phân số:
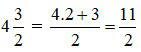
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số 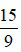 sang hỗn số
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó: