Số 40 được phân tích thành các thừa số nguyên tố là:
A. 40 = 4.10
B. 40 = 2.20
C. 40 = 22.5
D. 40 = 23.5
 Giải bởi Vietjack
Giải bởi Vietjack
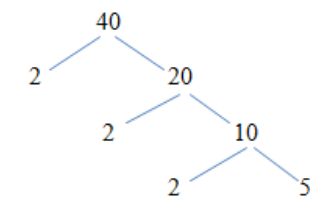
Vậy 40 = 2.2.2.5 = 23.5
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phép tính \[\overline {ab} .c = 424\]. Khi đó cc bằng bao nhiêu?
Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và 5?
Cho a2.b.7 = 140 với a, b là các số nguyên tố, vậy a có giá trị là bao nhiêu:
Một hình vuông có diện tích là 1936m2. Tính cạnh của hình vuông đó.
Số 360 khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
1. Số nguyên tố. Hợp số
− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
− Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.
Ví dụ:
+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.
+ Số 15 có bốn ước là 1; 3; 5; 15 nên 15 là hợp số.
Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
2. Phân tích một số ra thừa số nguyên tố
a. Thế nào là phân tích một số ra thừa số nguyên tố?
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Chú ý:
− Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
− Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
− Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
Ví dụ:
- Số 5 là số nguyên tố và dạng phân tích ra thừa số nguyên tố của nó là 5.
- Số 18 là hợp số và 18 được phân tích ra thừa số nguyên tố là:
18 = 2 . 3 . 3 (hoặc viết gọn là 18 = 2 . 32).
b. Cách phân tích một số ra thừa số nguyên tố
Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ: Số 76 được phân tích ra thừa số nguyên tố theo cột dọc như sau:
|
76 |
2 |
|
38 |
2 |
|
19 |
19 |
|
1 |
Vậy 76 = 22 . 19.
Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
Ví dụ: Số 36 được phân tích ra thừa số nguyên tố theo sơ đồ cây như sau:
Vậy 36 = 32 . 22.