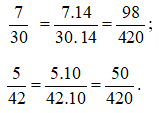Cho a; b có BCNN(a; b) = 630; ƯCLN(a; b) = 18. Có bao nhiêu cặp số
a; b thỏa mãn?
A. 6
B. 5
C. 2
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Vì ƯCLN(a;b) = 18 nên đặt a = 18x; b = 18y
với x; yN; ƯCLN(x; y) = 1; y ≠ 1.
Vì ƯCLN(a; b).BCNN(a; b) = a.b
Nên 18.630 = 18x.18y
⇒x.y = (18.630):(18.18) hay x.y = 35
mà y ≠ 1. Do đó ta có:
+) Nếu x = 1 thì y = 35 khi đó a = 18.1 = 18; b = 35.18 = 630
+) Nếu x = 5 thì y = 7 khi đó a = 18.5 = 90; b = 7.18 = 126
+) Nếu x = 7 thì y = 5 khi đó a = 18.7 = 126; b = 5.18 = 90
Vậy có ba cặp số a; b thỏa mãn.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm hai số tự nhiên a, b(a < b). Biết a + b = 20, BCNN(a, b) = 15.
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp 35 hay 40 học sinh lên một ô tô thì đều thấy thiếu mất 5 ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ 800 đến 900 em.
Cho tập hợp X là ước của 35 và lớn hơn 5. Cho tập Y là bội của 8 và nhỏ hơn 50. Gọi M là giao của 2 tập hợp X và Y, tập hợp M có bao nhiêu phần tử?
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng
BCNN(a,b) = 300.
Tìm số tự nhiên n lớn nhất có 3 chữ số sao cho n chia 8 dư 7, chia 31 dư 28.
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ 200 đến 300 bông.
Một số tự nhiên aa khi chia cho 7 dư 4; chia cho 9 dư 6. Tìm số dư khi chia a cho 63.
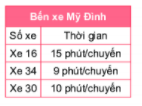
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác 0 của nó là 256.
Có bao nhiêu số tự nhiên x khác 0 thỏa mãn x∈BC(12;15;20) và x ≤ 100
Thực hiện các phép tính sau: \[\frac{3}{8} + \frac{5}{{24}}\]. Với kết quả là phân số tối giản
1. Bội chung
Một số được gọi là bội chung của hai hay nhiều số nếu nó là bội của tất cả các số đó.
Ví dụ: Ta có: B(9) = {0; 9; 18; 27; 36; 45; 54; 63; 72; …};
B(12) = {0; 12; 24; 36; 48; 60; 72; …}.
Hai tập hợp này có một số phần tử chung như 0; 36; 72; … Ta nói chúng là các bội chung của 9 và 12.
• Kí hiệu tập hợp các bội chung của a và b là BC(a, b).
• Tương tự, tập hợp các bội chung của a, b, c là BC(a, b, c).
Ví dụ:
- Tập hợp các bội chung của 15 và 55 là BC(15, 55).
- Tập hợp các bội chung của 16; 20; 25 là BC(16, 20, 25).
Cách tìm bội chung của hai số a và b:
- Viết tập hợp B(a) và bội B(b).
- Tìm những phần tử chung của B(a) và B(b).
Ví dụ:
Ta có: B(2) = {0; 2; 4; 6; 8; 10; 12; ...}
B(3) = {0; 3; 6; 9; 12; ...}
Những phần tử chung của B(2) và B(3) là 0; 6; 12; ...
Do đó BC(2, 3) = {0; 6; 12; ...}.
2. Bội chung nhỏ nhất
Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
Kí hiệu bội chung nhỏ nhất của a và b là BCNN(a, b).
Tương tự, bội chung nhỏ nhất của a, b và c là BCNN(a, b, c).
Nhận xét: Tất cả các bội chung của a và b đều là bội của BCN(a, b). Mọi số tự nhiên đều là bội của 1.
Do đó, với mọi số tự nhiên a và b (khác 0) ta có:
BCNN(a, 1) = a;
BCNN(a, b, 1) = BCNN(a, b).
Ví dụ:
• Ta có: BC(6, 8) = {0; 24; 48; 72; …} vì 24 là số nhỏ nhất khác 0 trong số các bội chung của 6 và 8, nên BCNN(6, 8) = 24.
Tất cả các bội chung của 6 và 8 (là 0; 24; 48; 72; …) đều là bội của BCNN(6, 8) là 24.
• BCNN(8, 1) = 1;
• BCNN(6, 8, 1) = BCNN(6, 8) = 24.
3. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Quy tắc:
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ví dụ: Tìm BCNN của 15 và 20.
Hướng dẫn giải
Ta có: 15 = 3 . 5; 20 = 22 . 5.
Thừa số nguyên tố chung và riêng là 2; 3 và 5.
Số mũ lớn nhất của 2 là 2; của 3 là 1 và của 5 là 1.
Do đó BCNN(15, 20) = 22 . 3 . 5 = 60.
Chú ý:
• Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.
Ví dụ: 3 và 8; 8 và 11; 11 và 3 là các cặp đôi một nguyên tố cùng nhau.
Khi đó, BCNN(3, 8, 11) = 3 . 8 . 11 = 264.
• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.
Ví dụ: Ta có BCNN(6, 12, 36) = 36 vì 36 ⋮ 9; 36 ⋮ 12 và 36 lớn hơn 9 và 12.
4. Ứng dụng trong quy đồng mẫu các phân số
Quy tắc:
Muốn quy đồng mẫu số nhiều phân số ta có thể làm như sau:
Bước 1: Tìm một bội chung của các mẫu số (thường là BCNN) để làm mẫu số chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu số (bằng cách chia mẫu số chung cho từng mẫu số riêng).
Bước 3: Nhân tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.
Ví dụ: Quy đồng mẫu số hai phân số 7/30 và 5/42.
Hướng dẫn giải
Ta có: 30 = 2 . 3 . 5; 42 = 2 . 3 . 7.
Thừa số nguyên tố chung và riêng là 2; 3; 5 và 7.
Số mũ lớn nhất của 2; 3; 5 và 7 đều là 1.
Khi đó, BCNN(30, 42) = 2 . 3 . 5 . 7 = 210.
Do đó BC(30; 42) = {0; 210; 420; ...}
Cách 1: Chọn mẫu chung là 210. Ta được:
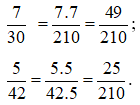
Cách 2: Chọn mẫu chung là một bội chung bất kì khác 0 của 30 và 42.
Chẳng hạn: chọn mẫu chung là 420, ta được: