A. n∈{−6; −1; 0; 5}
B. n∈{−1; 5}
C. n∈{0; 5}
D. n∈{1; 11}
Giải bởi Vietjack
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 2n+1∈U(11) = {±1; ±11}
Ta có bảng:
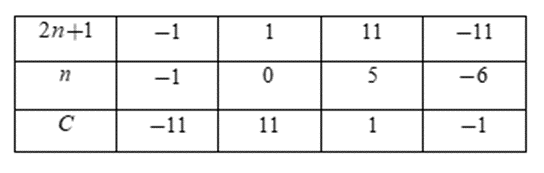
Vì C∈N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
1. Khái niệm phân số
Ta gọi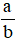 
, trong đó 
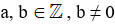là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số 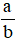đọc là a phần b.
Ví dụ 1. Phân số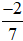 
có tử số là −2, mẫu số là 7 và được đọc là “âm hai phần bảy”.
Chú ý: Ta có thể dùng phân số để ghi (viết, biểu diễn) kết quả phép chia một số nguyên cho một số nguyên khác 0.
Ví dụ 2. Phân số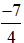 
là ghi kết quả phép chia −7 cho 4.
2. Phân số bằng nhau
Hai phân số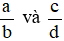 
được gọi là bằng nhau, viết là 
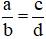, nếu a . d = b . c.
Ví dụ 3.
a)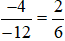 
vì (−4) . 6 = (−12) . 2 (cùng bằng –24).
b) 
không bằng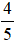 
, vì 3 . 5 không bằng 4 . 4. Viết 
.
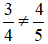Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số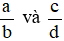
Ví dụ 4. Các cặp phân số sau có bằng nhau hay không?
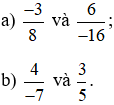
Lời giải:
a)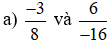 
So sánh hai tích: (−3) . (−16) và 8 . 6;
Ta có: (−3) . (−16) = 3 . 16 = 48 và 8 . 6 = 48.
Nên (−3) . (−16) = 8 . 6. Do đó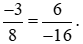 
.
.
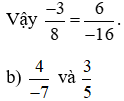So sánh hai tích: 4 . 5 và (−7) . 3;
Ta có: 4 . 5 = 20 và (−7) . 3 = −21.
Nên 4 . 5 ≠ (−7) . 3. Do đó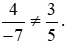 
.
Vậy hai phân số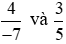 
không bằng nhau.
3. Biểu diễn số nguyên ở dạng phân số
Mỗi số nguyên n có thể coi là phân số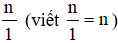 
. Khi đó số nguyên n được biểu diễn ở dạng phân số 
.
Ví dụ 5.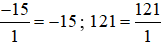 
.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
