Cho cấp số cộng với công sai khác 0. Biết rằng các số theo thứ tự đó lập thành cấp số nhân với công bội (q 0 ). Khi đó q bằng:
A. 1
B. 2
C. -1
D. -2
 Giải bởi Vietjack
Giải bởi Vietjack

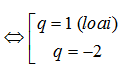
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho dãy số được xác định bởi ![]() . Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng
. Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng ![]() , với a,b,c là các số nguyên, . Khi đó có giá trị bằng
, với a,b,c là các số nguyên, . Khi đó có giá trị bằng
Dân số của thành phố A hiện nay là 3 triệu người. Biết rằng tỉ lệ tăng dân số hàng năm của thành phố A là 2% . Dân số của thành phố A sau 3 năm nữa sẽ là:
Cho cấp số nhân có công bội dương và biểu thức đạt giá trị nhỏ nhất. Tính
Ba số dương lập thành cấp số nhân, tích của số hạng thứ nhất và số hạng thứ ba bằng 36. Một cấp số cộng có n số hạng, công sai d = 4, tổng các số hạng bằng 510. Biết số hạng đầu của cấp số cộng bằng số hạng thứ 2 của cấp số nhân. Khi đó n bằng:
Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn một nửa). Khi đó khối lượng còn lại của 20 gam poloni 210 sau 7314 ngày là:
Ba số x;y;z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2;3;9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
I. Định nghĩa
- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un + 1 = un. q với .
- Đặc biệt
Khi q = 0, cấp số nhân có dạng u1, 0, 0, …., 0,…..
Khi q = 1, cấp số nhân có dạng u1, u1, u1, …., u1,…
Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..
- Ví dụ 1. Dãy số hữu hạn sau là một cấp số nhân: 2, 4, 8, 16, 32 với số hạng đầu u1 = 2 và công bội q = 2.
II. Số hạng tổng quát.
- Định lí: Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức: un = u1.qn - 1 với n ≥ 2.
- Ví dụ 2. Cho cấp số nhân (un) với u1 = – 1; q = – 2.
a) Tính u6;
b) Hỏi 128 là số hạng thứ mấy.
Lời giải:
a) Ta có: u6 = u1. q5 = –1. (– 2)5 = 32.
b) Ta có: un = u1.qn - 1 nên 128 = – 1. (– 2)n - 1
(– 2)^n - 1 = – 128 = (– 2)7.
n – 1 = 7 nên n = 8.
Vậy 128 là số hạng thứ 8.
III. Tính chất các số hạng của cấp số nhân
- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:
( hay ).
IV. Tổng n số hạng đầu của một cấp số nhân.
- Định lí: Cho cấp số nhân (un) với công bội q ≠ 1. Đặt Sn = u1 + u2 + …+ un .
Khi đó: .
- Chú ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1,….u1,….Khi đó, Sn = n.u1.
Ví dụ 3. Cho cấp số nhân (un) biết u1 = 3; u2 = 9. Tính tổng của 8 số hạng đầu tiên?
Lời giải:
Ta có: u2 = u1.q nên 9 = 3q.
Suy ra, công bội q = 3.
Khi đó, tổng của 8 số hạng đầu tiên là:
.