Số giao điểm của đồ thị hàm số với trục hoành là
A. 3
B. 0
C. 1
D. 4
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án C.
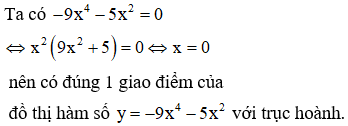
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình hộp chữ nhật có và (tham khảo hình vẽ). Góc giữa hai đường thẳng và AC bằng

Cho hình trụ có chiều cao bằng đường kính đáy, hai đáy là các hình tròn và . Gọi A là điểm di động trên đường tròn v à B là điểm di động trên đường tròn sao cho AB không là đường sinh của hình trụ . Khi thể tích khối tứ diện đạt giá trị lớn nhất thì đoạn thẳng AB có độ dài bằng
Cho khối nón có bán kính đáy bằng r và độ dài đường sinh bằng 3 lần bán kính đáy. Thể tích của khối nón đã cho bằng
Trong không gian Oxyz, cho mặt cầu và đường thẳng . Mặt phẳng chứa đường thẳng d và cắt mặt cầu theo giao tuyến là đường tròn có bán kính nhỏ nhất. Nếu phương trình của là thì
Cho hàm số . Tồn tại bao nhiêu số nguyên dương m để phương trình có 6 nghiệm thực phân biệt?
Giả sử rằng f là hàm số liên tục và thỏa mãn với mỗi , trong đó c là một hằng số. Giá trị của c thuộc khoảng nào trong các khoảng dưới đây?
Cho là hàm đa thức thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập . Giá trị của bằng
Bệnh máu khó đông ở người do đột biến gen lặn nằm trên nhiễm sắc thể giới tính X, alen trội tương ứng quy định người bình thường. Một gia đình có người chồng bình thường còn người vợ mang gen dị hợp về tính trạng trên. Họ dự định sinh 2 người con, giả thiết rằng mỗi lần sinh chỉ sinh được một người con, xác suất để cả 2 người con không bị bệnh máu khó đông là bao nhiêu?
Cho d là đường thẳng đi qua điểm và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị của hàm số tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.
Trong không gian Oxyz, cho điểm . Gọi lần lượt là hình chiếu vuông góc của M trên các trục tọa độ Ox, Oy, Oz. Mặt phẳng có phương trình là
Cho hình phẳng D giới hạn bởi các đường , trục hoành và hai đường thẳng và . Biết rằng diện tích của hình phẳng D bằng , với a, b là các số hữu tỷ. Mệnh đề nào dưới đây đúng?
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng . Cho hình lập phương có cạnh bằng . Tính theo a thể tích khối tứ diện .
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?