Tìm các giá trị của tham số \(m\) để đồ thị hàm số \(y = m{x^4} + \left( {2m - 1} \right){x^2} + m - 2\) chỉ có một cực đại và không có cực tiểu.
A.\(\left[ \begin{array}{l}m \le 0\\m >\frac{1}{2}\end{array} \right..\)
B.\(m \le 0.\)
C.\(\left[ \begin{array}{l}m \le 0\\m \ge \frac{1}{2}\end{array} \right..\)
D. \(m \le \frac{1}{2}.\)
Giải bởi Vietjack
Khi \(m = 0,\) hàm số trở thành \(y = - {x^2} - 2\) có đồ thị là một Parabol có bề lõm quay xuống nên hàm số có một cực đại và không có cực tiểu (thỏa mãn bài toán)
Khi \(m \ne 0,\) hàm số có một cực đại và không có cực tiểu khi và chỉ khi:
\(\left\{ \begin{array}{l}m < 0\\m\left( {2m - 1} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\2m - 1 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m \le \frac{1}{2}\end{array} \right. \Leftrightarrow m < 0.\)
Vậy hàm số có một cực đại và không có cực tiểu khi \(m \le 0.\)
Đáp án B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f\left( x \right) = 3\) là
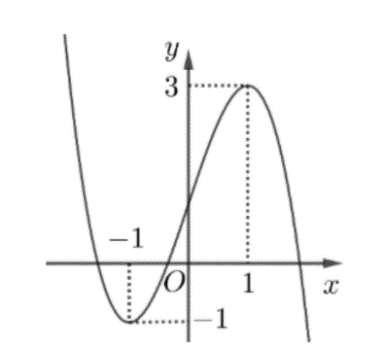
Cho hàm số có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số \(a,b,c,d?\)
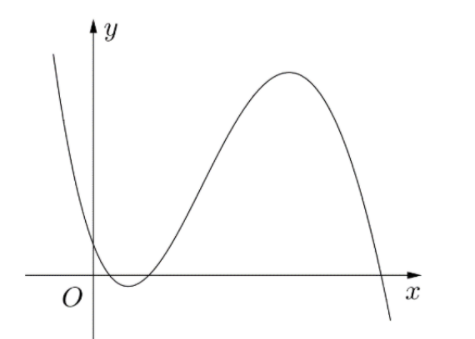
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào dưới đây đúng?
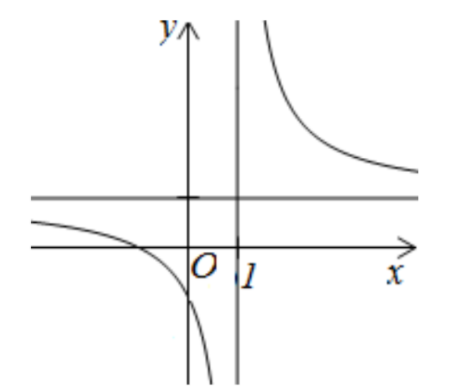
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng
Cho hàm số \(y = {x^3} + 3{x^2} + 1\) có đồ thị \(\left( C \right)\) và điểm \(A\left( {1;m} \right).\) Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để qua A có thể kể được đúng ba tiếp tuyến tới đồ thị \(\left( C \right).\) Số phần tử của \(S\) là
Cho các số dương \(a,b,c\) khác 1 thỏa mãn \({\log _a}\left( {bc} \right) = 3,{\log _b}\left( {ca} \right) = 4.\) Tính giá trị của \({\log _c}\left( {ab} \right).\)
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = {x^3} + 3{x^2} - 3\) song song với trục hoành?
Biết \({\log _a}b = 2,{\log _a}c = 3;\) với \(a,b,c >0;a \ne 1.\) Khi đó giá trị của \({\log _a}\left( {\frac{{{a^2}\sqrt[3]{b}}}{c}} \right)\) bằng
Một cấp số cộng có \({u_1} = - 3,{u_8} = 39.\) Công sai của cấp số cộng đó là
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc và \(OA = OB = OC = a.\) Khi đó thể tích của khối tứ diện \(OABC\) là
Gọi \(d\) là đường thẳng đi qua \(A\left( {2;0} \right)\) có hệ số góc \(m\left( {m >0} \right)\) cắt đồ thị tại ba điểm phân biệt \(A,B,C.\) Gọi \(B',C'\) lần lượt là hình chiếu vuông góc của \(B,C\) lên trục tung. Biết rằng hình thang \(BB'C'C\) có diện tích bằng 8, giá trị của \(m\) thuộc khoảng nào sau đây?
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(AB = AC = a,\) góc \(BAC = {120^0},AA' = a.\) Gọi \(M,N\) lần lượt là trung điểm của \(B'C'\) và \(CC'.\) Số đo góc giữa mặt phẳng \(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng
Cho một đa giác đều có 18 đỉnh nội tiếp đường tròn tâm \(O.\) Gọi \(X\) là tập hợp tất cả các tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho. Chọn 1 tam giác trong tập hợp \(X.\) Xác suất để tam giác được chọn là tam giác cân bằng
Giá trị của biểu thức \(A = {2^{{{\log }_4}9 + {{\log }_2}5}}\) là
Giá trị lớn nhất của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\) là
