Cho hình chóp đều S.ABCD có cạnh đáy bằng a√2, cạnh bên bằng 2a. Gọi α là góc tạo bởi hai mặt phẳng (SAC) và (SCD). Tính cosα.
A.√212.
B.√2114.
C.√213.
D. √217.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
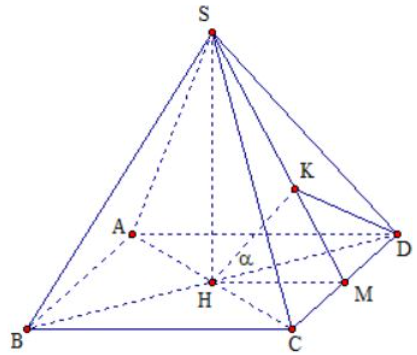
Gọi H là hình chiếu của S trên mặt phẳng (ABCD). Hình chóp S.ABCD đều nên H là tâm hình vuông ABCD,(SAC)∩(ABCD)=AC và SH⊥(ABCD)⇒(SAC)⊥(ABCD).
Ta có: HD⊥AC⇒HD⊥(SAC).(1)
Gọi M là trung điểm của CD, suy ra: {CD⊥HMCD⊥SH⇒CD⊥(SHM) mà CD⊂(SCD).
{(SCD)⊥(SHM)(SCD)∩(SHM)=SM nên từ H kẻ đường thẳng vuông góc với SM tại K, suy ra HK⊥(SCD)(2)
Từ (1) và (2) suy ra: α=((SAC),(SCD))=(HD,HK)=^KHD.
Tam giác KHD vuông tại K có HD=12BD=12a√2.√2=a.
1HK2=1HM2+1SH2=1HM2+1SD2−HD2=2a2+14a2−a2=73a2⇒HK=a√217.
Vậy cosα=HKHD=√217.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tứ diện SABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA=3a,SB=4a,SC=5a. Tính theo a thể tích V của khối tứ diện SABC.
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=a,AD=2a,SA vuông góc với mặt phẳng đáy và SA=a√3. Thể tích khối chóp S.ABCD bằng
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=m3x3−2mx2+(3m+5)x đồng biến trên R.
Cho hàm số f(x) xác định và liên tục trên R. Đồ thị hàm số f′(x) như hình vẽ dưới đây
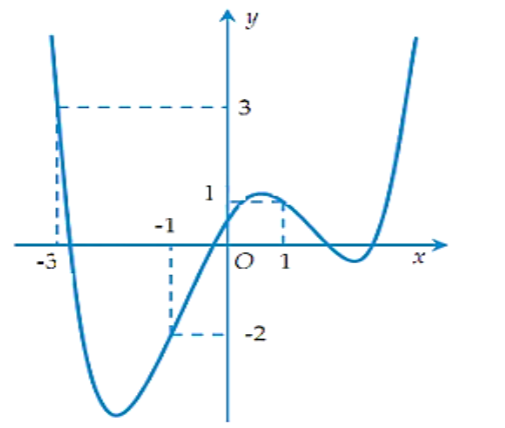
Xét hàm số g(x)=f(x)−13x3−34x2+32x+2019. Trong các mệnh đề sau:
(I)g(0)<g(1).
(II)min
\left( {III} \right) Hàm số g\left( x \right) nghịch biến trên \left( { - 3; - 1} \right).
\left( {IV} \right)\mathop {\max }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = \mathop {\max }\limits_{\left[ { - 3;1} \right]} \left\{ {g\left( { - 3} \right);g\left( 1 \right)} \right\}.
Số mệnh đề đúng là
Cho hàm số y = f'\left( x \right) có đồ thị như hình vẽ.
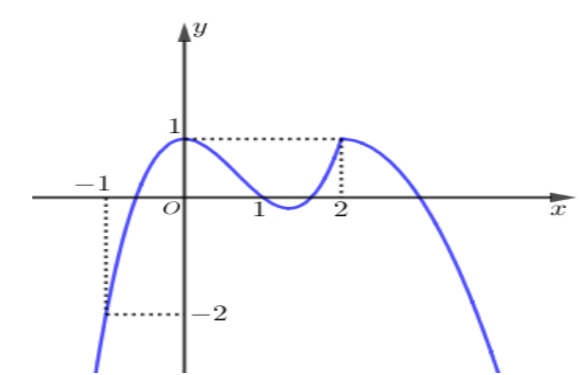
Hàm số g\left( x \right) = f\left( {{x^2}} \right) - \frac{{{x^6}}}{3} + {x^4} - {x^2} đạt cực tiểu tại bao nhiêu điểm?
Cho cấp số nhân \left( {{u_n}} \right) có {u_1} = 2 và công bội q = 2. Tính {u_3}?
Cho hai dãy ghế đối diện nhau mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
Giá trị lớn nhất của hàm số f\left( x \right) = {x^3} - 8{x^2} + 16x - 9 trên đoạn \left[ {1;3} \right] là
Cho hàm số y = - {x^4} + 2{x^2} có đồ thị như hình vẽ.
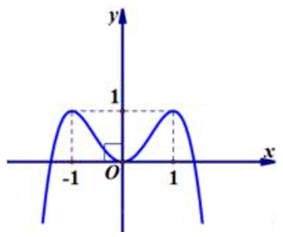
Tìm tất cả các giá trị thực của m để phương trình - {x^4} + 2{x^2} = m có hai nghiệm phân biệt.
Tìm hệ số h của số hạng chứa {x^5} trong khai triển {\left( {{x^2} + \frac{2}{x}} \right)^7}?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC = 2ES. Gọi \left( \alpha \right) là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD,\left( \alpha \right) cắt hai cạnh SB,SD lần lượt tại M,N. Tính theo V thể tích khối chóp S.AMEN.
Cho hàm số y = f\left( x \right) liên tục trên đoạn \left[ { - 4;4} \right] và có bảng biến thiên trên đoạn \left[ { - 4;4} \right] như sau
![Cho hàm số y=f(x) liên tục trên đoạn [-4;4] và có bảng biến thiên trên đoạn [-4;4] như sau. Phát biểu nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1651165933/1651166122-image8.png)
Phát biểu nào sau đây đúng?
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a,SA \bot \left( {ABC} \right), góc giữa đường thẳng SB và mặt phẳng \left( {ABC} \right) bằng {60^0}. Khoảng cách giữa hai đường thẳng AC và SB bằng:
Cho hàm số y = f\left( x \right) có bảng biến thiên như sau
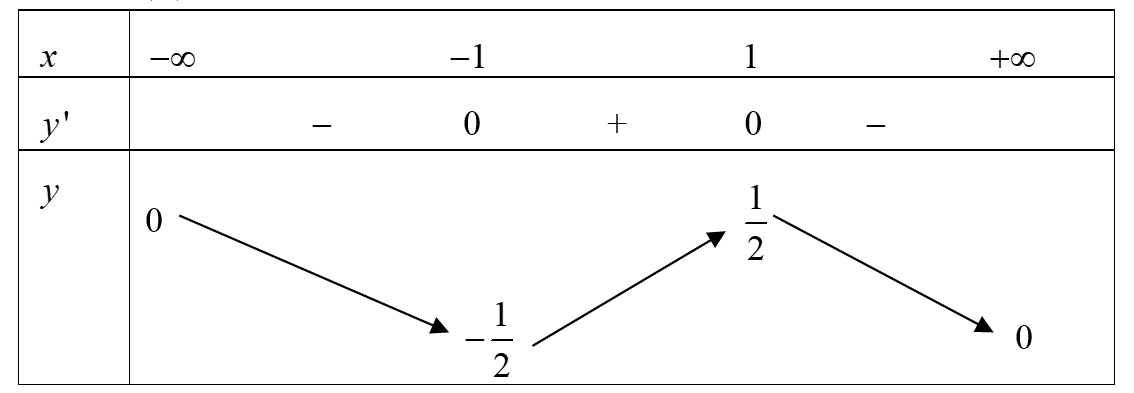
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là M,m. Giá trị biểu thức P = {M^2} + {m^2} bằng