Một chất điểm A xuất phát từ O chuyển động với quy luật , trong đó s(t) là quãng đường chất điểm đi được trong khoảng thời gian t kể từ thời điểm xuất phát. Cùng thời điểm đó, một chất điểm B ở cách O 30m, đang di chuyển cùng hướng A với vận tốc 10m/s thì lại chuyển động với gia tốc . Tại thời điểm hai vật gặp nhau, vận tốc chất điểm A bằng
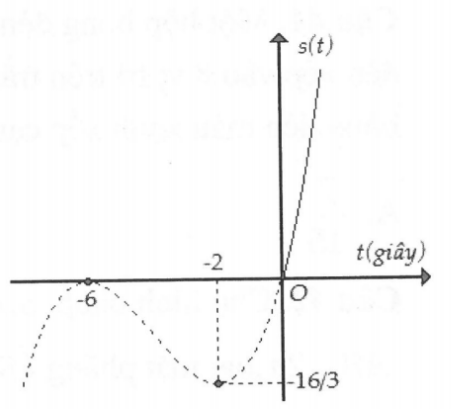
A. 30m/s.
B. 38,5m/s.
C. 48m/s.
D. 22,5m/s.
 Giải bởi Vietjack
Giải bởi Vietjack


Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy là hình chữ nhật BC= a, tam giác SAB đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng
Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB=a,BC=2a và độ dài các cạnh bên bằng 3a/2. Thể tích khối chóp đã cho bằng
Cho hình trụ (T) có bán kính đáy r=2 và diện tích xung quanh . Thể tích khối trụ (T) bằng
Cho đa giác lồi 10 cạnh. Có bao nhiêu tam giác được tạo thành từ các đỉnh của đa giác đã cho?
Cho hàm số f(x) có đạo hàm liên tục trên R\{0} và thỏa mãn 2f(2x)-f(1/x)= . Giá trị dx bằng
Cho hình lăng trụ đứng ABC.A' B' C' có đáy là tam giác vuông cân đỉnh A, BC=2a, thể tích khối lăng trụ đã cho bằng . Khoảng cách từ điểm B' đến mặt phẳng (A' BC) bằng
Cho a là số thực dương khác 1 và x,y là các số thực dương. Mệnh đề nào dưới đây đúng?
Cho hình chóp đều S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AB=2a, hai mặt phẳng (SAB),(SAD) vuông góc với mặt phẳng đáy, SB= a, M là điểm thỏa mãn . Giá trị cosin góc giữa hai mặt phẳng (MAB) và (MBC) bằng
Một khối thủy tinh có dạng khối nón có chiều cao bằng 20 cm, bán kính đáy bằng 5 cm. Anh A cần cắt gọt khối thủy tinh trên để tạo thành một viên thủy tinh mới có dạng khối lăng trụ tứ giác đều. Thể tích lớn nhất của viên thủy tinh mới gần giá trị nào dưới đây?
Cho các số thực x,y dương thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
Cho số phức z=a+bi (a,b∈R) thỏa mãn ||=2|z+2i|. Khi biểu thức P=|iz+4-3i| đạt giá trị lớn nhất thì a-b bằng
Trong không gian Oxyz, cho các điểm A(a;0;0),B(0;b;0),C(0;0;c) di động trên các trục Ox,Oy,Oz sao cho 2a+b-c-6=0 và hai điểm M(2;-3;5),N(-1;0;-1). Xét các mặt cầu (S) ngoại tiếp tứ diện OABC có tâm I. Khi || đạt giá trị nhỏ nhất thì mặt cầu (S) có diện tích bằng
Cho hình chóp đều S.ABCD có cạnh đáy bằng , cạnh bên bằng . Gọi M là trung điểm CD. Khoảng cách giữa hai đường thẳng AC và SM bằng
Một món quà lưu niệm có dạng khối cầu bán kính bằng 5cm được làm bằng thủy tinh, bên trong khối cầu đó người ta đúc một kim tự tháp có dạng khối đa diện đều loại {3;3} bằng đồng. Biết các đỉnh của kim tự tháp nằm trên mặt cầu đã cho, giá 1 thủy tinh là a (triệu đồng) và giá 1 là 10a (triệu đồng). Chi phí nguyên vật liệu để làm món quà đã cho gần với giá trị nào dưới đây?