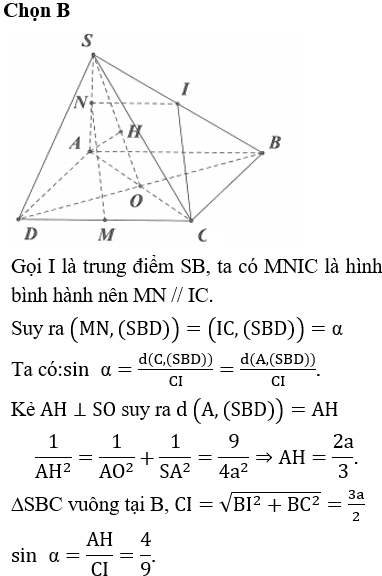
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=2a và vuông góc với đáy. Gọi M, N lần lượt là trung điểm của CD và SA. Tính sin góc tạo bởi đường thẳng MN và mặt phẳng (SBD).

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết SA⊥(ABC) và SA=a$\sqrt{3}$. Tính theo a thể tích của khối chóp S.ABC.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a$\sqrt{3}$ và vuông góc với đáy. Gọi G là trọng tâm tam giác BCD. Tính khoảng cách từ G đến mặt phẳng (SBC).

Cho tam giác ABC có BC=a,AC=b,AB=c và bán kính đường tròn ngoại tiếp tam giác ABC bằng R. Tìm khẳng đính sai trong các khẳng định sau?

Cho hàm số $\mathrm{y}=\frac{-\mathrm{mx}+3}{3\mathrm{x}-\mathrm{m}}$ với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S

Có bao nhiêu giá trị nguyên của tham số m∈[-10;10] để hàm số y=|2${\mathrm{x}}^4-2{\mathrm{x}}^3-{\mathrm{x}}^2+\mathrm{m}$| có 5 điểm cực trị 

Cho hai số phức z,w thỏa mãn |z+2w|=4,|z-2w|=2,|3z+w|=3. Tìm giá trị của biểu thức P=$\overline{\mathrm{z} }\mathrm{w}+\mathrm{z}\overline{\mathrm{w}}.$

Cho  hàm số $\mathrm{y}={\mathrm{x}}^3+2(\mathrm{m}+1){\mathrm{x}}^2+3\mathrm{mx}+2$ có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y=-x +2 cắt đồ thị (C ) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2$\sqrt{6}$.

Cho x>0; y>0 thỏa mãn $\ln \left({\mathrm{xy}}^2\right)=8; \ln \frac{\mathrm{x}}{\mathrm{y}}=-1$. Tính P=ln⁡(xy).

Cho hàm số $\mathrm{y}={\mathrm{ax}}^3+{\mathrm{bx}}^2+\mathrm{cx}+\mathrm{d}$ (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:

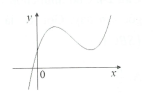
Khẳng định nào sau đây là khẳng định đúng?  

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x–y+z -1= 0 và (Q):2x+y+1= 0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng  (P) và (Q).

Biết $\frac{\mathrm{a}}{\mathrm{b}}$ (trong đó $\frac{\mathrm{a}}{\mathrm{b}}$  là phân số tối giản, a,b∈ ${\mathrm{N}}^{*}$) là giá trị thực của tham số m để hàm số  $\mathrm{y}=2{\mathrm{x}}^3-3{\mathrm{mx}}^2-6(3{\mathrm{m}}^2-1)\mathrm{x}+2018$ có hai điểm cực trị x1;x2 thỏa mãn ${\mathrm{x}}_1{\mathrm{x}}_2+2({\mathrm{x}}_1+{\mathrm{x}}_2)=1$. Tính P= a+2b.

Cho các số thực x,y thay đổi thỏa mãn${\log }_2\frac{\mathrm{sinx}+2}{\mathrm{cosx}+2}=2\mathrm{cosx}-\mathrm{sinx}+3$. Gọi -$\frac{\mathrm{a}}{\mathrm{b}} \mathrm{với} \mathrm{a}\in \mathrm{N}*,\mathrm{b}\in \mathrm{N}*,\frac{\mathrm{a}}{\mathrm{b}}$ tối giản là giá trị nhỏ nhất của biểu thức P=$3{\cos }^3\mathrm{x}+\sin 2\mathrm{x}-5\mathrm{cosx}$. Tính T=a+b. 

Biết ${\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=3$ và${\int }_{\mathrm{b}}^{\mathrm{a}}\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}=5$. Tính I=${\int }_{\mathrm{a}}^{\mathrm{b}}\left[3\mathrm{f}\right(\mathrm{x})+2\mathrm{g}(\mathrm{x}\left)\right]\mathrm{dx}$

Biết rằng ${\int }_0^{\frac{\mathrm{\pi }}{4}}(2\mathrm{x}+{\cos }^2\mathrm{x})\mathrm{dx}={\mathrm{a\pi }}^2+\mathrm{b\pi }+\mathrm{c}$, với a,b,c là các số hữu tỉ. Tính P=$\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{1}{\mathrm{c}}$.

Cho hàm số $\mathrm{y}={\mathrm{x}}^3-3{\mathrm{x}}^2-9\mathrm{x}$. Khẳng định nào sau đây là khẳng định đúng?