Họ các nguyên hàm của hàm số $f\left(x\right)=3x^2+1$ là

Số phức liên hợp của số phức z=3+4i là

Tiếp tuyến của đồ thị hàm số $y=x^3-3x^2+2$ tại điểm M(-1;-2) là

Cho biết $\underset{x\to 1}{lim}\frac{\sqrt{a{x}^2+1}-bx-2}{x^3-3x+2}$ $(a,b\in R)$ có kết quả là một số thực. Giá trị của biểu thức $a^2+b^2$ bằng

Cho hình chóp S.ABCD có đáy là hình thang cân AB=2a,BC=CD=DA=a. Cạnh bên SA=$\sqrt{3}a$ vuông góc với đáy. Côsin góc giữa hai mặt phẳng (SAD) và (SBC) bằng

Gọi M,N lần lượt là các điểm biểu diễn của $z_1,z_2$, trong đó $z_1,z_2$ là nghiệm phức của phương trình $z^2+3z+3=0$. Tính diện tích tam giác OMN.

Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,SA=SB,SC=SD. Biết (SAB)$\perp$(SCD) và tổng diện tích của hai tam giác SAB,SCD bằng $\frac{7a^2}{10}$. Tính thể tích V của khối chóp S.ABCD.

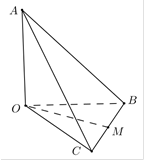
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Gọi M là trung điểm cạnh BC. Côsin góc giữa hai đường thẳng AB và OM  bằng

Cho hàm số $y=-x^4+(2m+\frac{1}{2})x^2$ có đồ thị (C). Tổng tất cả các giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này cũng đi qua điểm A($\frac{9}{8}$;9/8) là

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(4;0;1),B(-2;2;3). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB?

Cho hàm số f(x) liên tục trên R thoả mãn f(0)=0 và $\left|f\right(x)-f(y\left)\right|\le |\sin x-\sin y|$ với mọi $x,y\in R$. Giá trị lớn nhất của tích phân ${\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\right(f\left(x\right){)}^2-f\left(x\right))dx$ bằng

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng $\Delta$:$\frac{x-m}{1}=\frac{y+1}{-2}=\frac{z+m^2}{1}$ và hai điểm M(-1;4;1),N(3;-2;0). Gọi H, K lần lượt là hình chiếu vuông góc của M, N lên Δ. Khối tứ diện HKMN có thể tích nhỏ nhất bằng

Hàm số $y=-x^3+3x$ đồng biến trên khoảng nào dưới đây ?

Khối chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA,AB. Thể tích khối chóp S.MNP là

Một tổ hợp chập 2 của tập A={1,2,...,10} là

Trong không gian với hệ toạ độ Oxyz, cho điểm M(4;3;2). Có bao nhiêu mặt phẳng qua M cắt ba trục toạ độ Ox,Oy,Oz lần lượt tại A,B,C sao cho 6OA=2OB=3OC>0.