Tịnh tiến liên tiếp đồ thị hàm số y=$\frac{-5}{x+2}$ theo trục Oy lên trên 2 đơn vị và theo Ox sang trái 3 đơn vị ta được đồ thị hàm số $y=g\left(x\right)$. Có bao nhiêu điểm trên đồ thị $y=g\left(x\right)$ có các tọa độ đều là số nguyên?

Hàm số y=sinx đồng biến trên khoảng nào?

Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB=a, $AC=a\sqrt{2}$, $AD=a\sqrt{3}$. Khoảng cách d từ điểm A đến mặt phẳng (BCD) là

Phương trình tiếp tuyến của đồ thị hàm số $y=x^3-2x+3$ tại điểm có hoành độ x=2 là

Hai xạ thủ bắn mỗi người một viên đạn vào bia một cách độc lập. Biết xác xuất trúng của xạ thủ thứ nhất và xạ thủ thứ hai lần lượt là 0,9 và 0,7. Xác suất để có ít nhất một xạ thủ bắn trùng bia là

Xếp ngẫu nhiên 6 học sinh nam và 3 học sinh nữ thành một hàng ngang. Tính xác suất để có đúng 2 học sinh nam đứng xen kẽ với 3 học sinh nữ

Cho mặt cầu có diện tích bằng $16\pi \left(c{m}^2\right).$ Đường kính mặt cầu đó là

Hàm số nào dưới đây đồng biến trên khoảng $\left(0;+\infty \right)$?

Cho hình nón đỉnh S đáy là đường tròn tâm O bán kính R=5, góc ở đỉnh bằng ${60}^o$. Một mặt phẳng đi qua đỉnh S cắt đường tròn đáy tại hai điểm A và B sao cho AB=8. Tính khoảng cách từ O đến (SAB).

Gọi a là số thực, a>1 sao cho phương trình $a^x={\log }_{a}x$ có nghiệm duy nhất. Chọn mệnh đề đúng.

Cho tứ diện ABCD. Gọi G là trọng tâm $\Delta ACD$ và M là điểm trên cạnh AC sao cho $\frac{AM}{AC}=\frac{4}{5}$

Tính $\frac{V_{ABMG}^{}}{V_{ABCD}^{}}$ 

Giải bất phương trình ${\log }_3\left(4x-1\right)<1$.

Một chiếc hộp hình hộp chữ nhật ABCD.EFGH, mặt trên EFGH không có nắp (xem

hình bên).

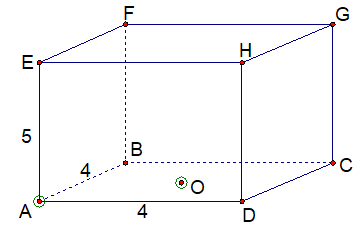
Có một con kiến ở đỉnh A  bên ngoài hộp và một miếng mồi của kiến tại điểm O là

tâm đáy ABCD ở bên trong hộp. Tính quãng đường ngắn nhất mà con kiến tìm đến

miếng mồi (làm tròn đến một chữ số thập phân).

Tìm m để phương trình $m\cos x+\sin x=1-m$ có nghiệm

Cho tứ diện ABCD có cạnh AD=3 và các cạnh còn lại bằng 2. Mệnh đề nào sau đây đúng

Cho hàm số $y=x^3-x$ có đồ thị (C). Gọi M,N là hai điểm phân biệt trên (C) và các tiếp tuyến tại M,N song song với nhau. Tính $x_M+x_N$.