Chọn đáp án đúng.
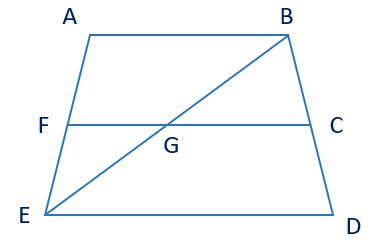
A. \[\widehat {ABC}\]và \[\widehat {CDE}\] là hai góc kề nhau;
B. \[\widehat {BGC}\] và \[\widehat {FGE}\] là hai góc kề nhau;
C. \[\widehat {CGE}\]và \[\widehat {FGB}\] là hai góc kề nhau;
D. \[\widehat {CGE}\] và \[\widehat {EGF}\] là hai góc kề nhau.
Giải bởi Vietjack
Đáp án đúng là: D
Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.
\[\widehat {ABC}\]và \[\widehat {CDE}\] là hai góc có chung một cạnh BD nhưng không có đỉnh chung;
\[\widehat {BGC}\] và \[\widehat {FGE}\] là hai góc đối đỉnh;
\[\widehat {CGE}\]và \[\widehat {FGB}\] là hai góc đối đỉnh;
\[\widehat {CGE}\] và \[\widehat {EGF}\] là hai góc kề nhau vì có cạnh chung EG và có đỉnh chung.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 110^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
Cho \(\widehat {xOy} = 120^\circ \), tia Ot là tia phân giác của góc xOy. Tính số đo góc xOt
Cho hình chữ nhật ABCD như hình vẽ. Biết IJ // AB và \[\widehat {JOC} = 30^\circ \].
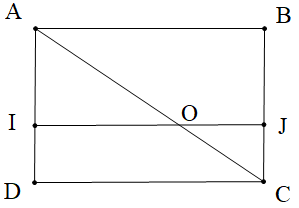
Số đo góc BAC là:
Cho hình bình hành ABCD như hình vẽ. Biết EF // DC, \[\widehat {DAB} = 65^\circ \] và \[\widehat {AFE} = 35^\circ \]. Số đo góc KAD là:
Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:
Viết giả thiết cho định lí sau:
“Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
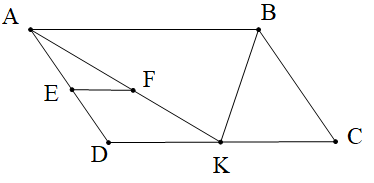
Cho hình vẽ. Tính góc FEC, biết EF // BC và \[\widehat {ECB} = 40^\circ \]:
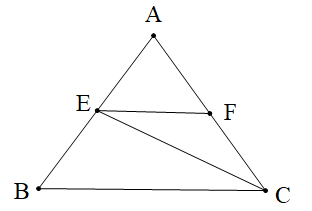
Cho các phát biểu sau:
(1) Hai góc dối đỉnh thì bằng nhau;
(2) Hai bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Nếu N là trung điểm của HK thì NH = NK;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
Cho ba đường thẳng phân biệt a, b và c, biết a // b và \[a \bot c\]. Kết luận nào đúng:
