Trắc nghiệm Toán 7 Bài tập cuối chương 4 có đáp án
-
439 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ. Tính góc FEC, biết EF // BC và \[\widehat {ECB} = 40^\circ \]:
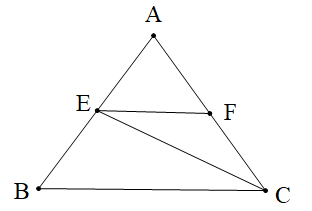
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì EF // BC nên ta có: \[\widehat {ECB}\] và \[\widehat {FEC}\] là hai góc so le trong
Suy ra \[\widehat {FEC} = \widehat {ECB} = 40^\circ \]
Vậy \[\widehat {FEC} = 40^\circ \].
Câu 2:
Cho hình thoi ABCD như hình vẽ.
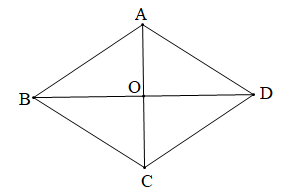
Chọn phương án đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
\[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh là phát biểu đúng, chọn phương án A;
\[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc kề bù;
\[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc trong cùng phía.
\[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.
Câu 3:
Cho hình chữ nhật ABCD như hình vẽ. Biết IJ // AB và \[\widehat {JOC} = 30^\circ \].
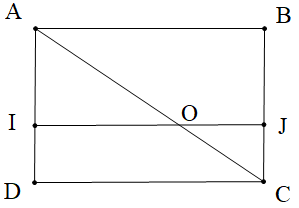
Số đo góc BAC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Vì AB // IJ nên ta có: \[\widehat {JOC}\] và \[\widehat {BAC}\] là hai góc đồng vị
Suy ra \[\widehat {BAC} = \widehat {JOC} = 30^\circ \] (1)
Vậy \[\widehat {BAC} = 60^\circ \].
Câu 4:
Cho hình bình hành ABCD như hình vẽ. Biết EF // DC, \[\widehat {DAB} = 65^\circ \] và \[\widehat {AFE} = 35^\circ \]. Số đo góc KAD là:
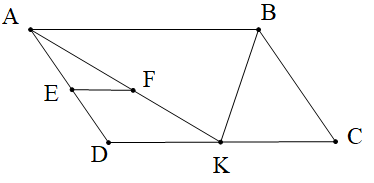
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì ABCD là hình bình hành nên AB // DC do đó \(\widehat {BAK} = \widehat {AKD}\) (hai góc so le trong).
Vì EF // DC nên \[\widehat {AFE} = \widehat {AKD}\] (hai góc đồng vị)
Suy ra \(\widehat {BAK} = \widehat {AFE}\) (cùng bằng góc \(\widehat {AKD}\))
Mà \[\widehat {AFE} = 35^\circ \Rightarrow \widehat {BAK} = 35^\circ \]
Mà \[\widehat {BAK} + \widehat {KAD} = \widehat {DAB}\] (vì tia AK nằm giữa hai tia AB và AD)
\[ \Rightarrow \widehat {KAD} = \widehat {DAB} - \widehat {KAB} = 65^\circ - 35^\circ = 30^\circ \]
Vậy \[\widehat {KAD} = 30^\circ \].
Câu 5:
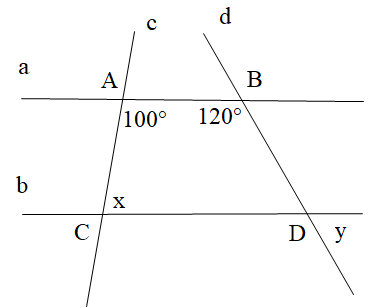
Cho hình vẽ dưới đây, biết a // b. Tính x, y.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì a // b nên \[\widehat {BAC} + \widehat {ACD} = 180^\circ \] (hai góc trong cùng phía bù nhau)
Suy ra 100o + x = 180o
Do đó x = 180o ‒ 100° = 80°
Vì a // b nên \[\widehat {ABD} + \widehat {CDB} = 180^\circ \] (hai góc trong cùng phía bù nhau)
Suy ra \[\widehat {CDB} = 180^\circ - \widehat {ABD}\]
\[\widehat {CDB} = 180^\circ - 120^\circ = 60^\circ \]
Mà góc y và \(\widehat {CDB}\) là hai góc đổi đỉnh nên \[y = \widehat {CDB} = 60^\circ \]
Vậy x = 80° và y = 60°.
Câu 6:
Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 110^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
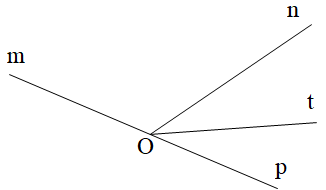
Vì \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù nên \[\widehat {mOn} + \widehat {nOp} = 180^\circ \]
Suy ra \[\widehat {nOp} = 180^\circ - \widehat {mOn}\]
Hay \[\widehat {nOp} = 180^\circ - 110^\circ = 70^\circ \]
Mà \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2}\] (vì Ot là tia phân giác góc nOp)
Suy ra \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2} = \frac{{70^\circ }}{2} = 35^\circ \]
Vì hai góc mOn và nOp là hai góc kề bù nên tia On nằm giữa hai tia Om và Op; tia Ot là phân giác của góc nOp nên tia Ot nằm giữa hai tia On và Op.
Do đó tia Ot nằm giữa hai tia On nằm giữa hai tia Om và Ot
Suy ra \[\widehat {mOt} = \widehat {mOn} + \widehat {nOt}\] suy ra \[\widehat {mOt} = 110^\circ + 35^\circ = 145^\circ \]
Vậy \[\widehat {mOt} = 145^\circ \].
Câu 7:
Cho góc AOB và OI tia phân giác của góc đó. Vẽ tia phân giác OJ của góc BOI. Biết \[\widehat {IOJ} = 25^\circ \]. Số đo góc AOB là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
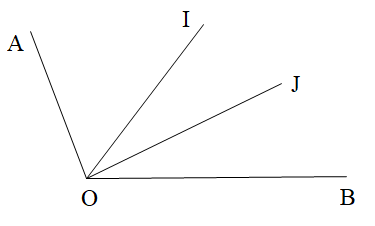
Ta có:
\[\widehat {B{\rm{OJ}}} = \widehat {JOI} = 25^\circ \] (vì OJ là tia phân giác góc IOB)
Suy ra \[\widehat {IOB} = \widehat {B{\rm{OJ}}}{\rm{ + }}\widehat {JOI} = 25^\circ + 25^\circ = 50^\circ \]
Lại có: \[\widehat {AOI} = \widehat {IOB} = 50^\circ \] (vì OI là tia phân giác góc AOB)
Suy ra \[\widehat {AOB} = \widehat {AOI} + \widehat {IOB} = 50^\circ + 50^\circ = 100^\circ \]
Vậy \[\widehat {AOB} = 100^\circ \].
Câu 8:
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”. Giả thiết, kết luận của định lí là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOI. Kết luận \[OI \bot OK\].
Câu 9:
Khi chứng minh định lí, người ta cần:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Khi chứng minh định lí, ta cần chứng minh định lý đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.
Câu 10:
Cho các phát biểu sau:
(1) Hai góc dối đỉnh thì bằng nhau;
(2) Hai bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Nếu N là trung điểm của HK thì NH = NK;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
(1) Hai góc dối đỉnh thì bằng nhau. Đây là phát biểu đúng.
(2) Hai bằng nhau thì đối đỉnh. Đây là phát biểu sai.
Vì tồn tại hai góc bằng nhau, mà không chung đỉnh thì đó không phải hai góc đối đỉnh như hình sau:
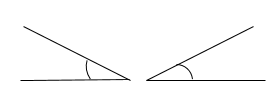
(3) Hai đường thẳng song song thì cắt nhau. Đây là phát biểu sai.
Vì hai đường thẳng song song thì không cắt nhau.
(4) Nếu N là trung điểm của HK thì NH = NK. Đây là phát biểu đúng.
(5) Nếu NH = NK thì N là trung điểm của HK. Đây là phát biểu sai.
Vì nếu M, H, K không thẳng hàng thì NH = NK không suy ra được N là trung điểm của HK
Câu 11:
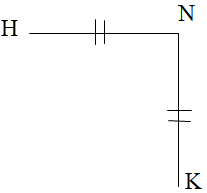
Cho hình vẽ.
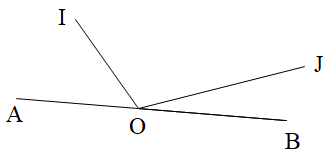
Góc AOI và góc IOB là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Góc AOI và góc IOB là hai góc kề bù vì tổng số đo hai góc bằng 180o.
Câu 12:
Cho hình vẽ.
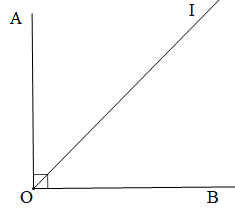
Biết OI là tia phân giác góc AOB. Số đo góc AOI là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nhìn hình ta thấy \[\widehat {AOB} = 90^\circ \]
Suy ra\[\widehat {AOI} = \widehat {IOB} = \frac{{\widehat {AOB}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \] (vì OI là tia phân giác góc AOB).
Vậy \(\widehat {AOI} = 45^\circ \).
Câu 13:
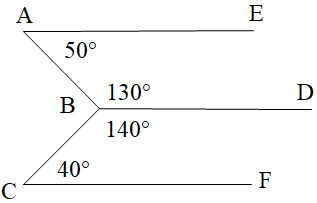
Cho hình vẽ sau
 Xem đáp án
Xem đáp án
Chọn đáp án đúng:
A. AE // BD;
B. BD // CF;
C. Cả A và B đều sai;
D. Cả A và B đều đúng.
Hướng dẫn giải
Đáp án đúng là: D

Vì
\[\widehat A + \widehat {ABD} = 50^\circ + 130 = 180^\circ \] mà hai góc ở vị trí trong cùng phía nên AE // BD
Vì \[\widehat {CBD} + \widehat C = 140^\circ + 40 = 180^\circ \] mà hai góc ở vị trí trong cùng phía nên BD // CF
Vậy cả A, B đều đúng.
Câu 14:
Hai đường thẳng xy và x’y’ cắt nhau tại O. Góc đối đỉnh của \[\widehat {xOy'}\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
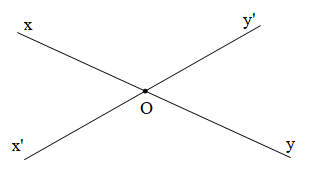
Vì hai đường thẳ
ng xy và x’y’ cắt nhau tại O nên Oy là tia đối của tia Ox, Oy’ là tia đối của tia Ox’.
Vậy góc đối đỉnh với góc \[\widehat {xOy'}\] là \[\widehat {x'Oy}\].
Câu 15:
Cho ba đường thẳng phân biệt a, b và c, biết a // b và \[a \bot c\]. Kết luận nào đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
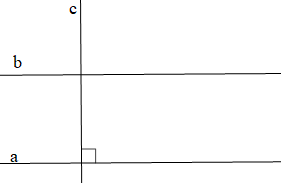
Ta có: \[\left\{ {\begin{array}{*{20}{c}}{a//b}\\{a \bot c}\end{array}} \right. \Rightarrow b \bot c\] (quan hệ tính vuông góc với tính song song)
Câu 16:
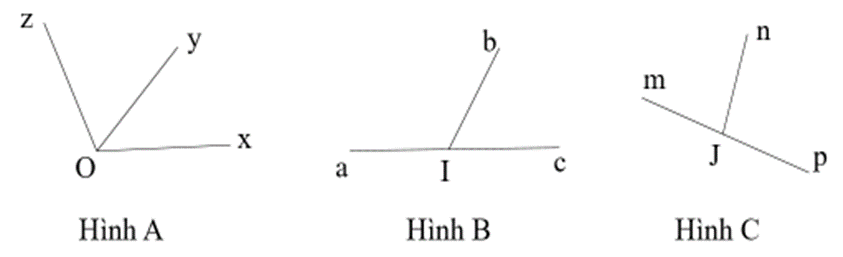
Trong các hình dưới đây hình nào là 2 góc kề bù.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hình B và C là hai góc kề bù vì chúng là hai góc kề nhau và tổng số đo 2 góc bằng 180o.
Câu 17:
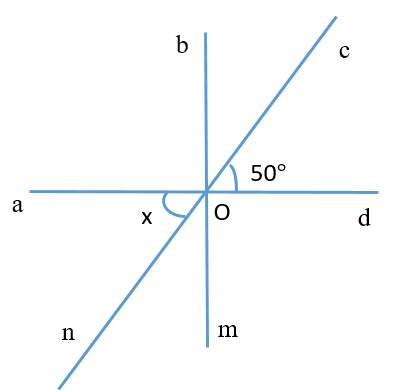
Tìm số đo x
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai góc \(\widehat {aOn}\) và \(\widehat {cOd}\) là hai góc đối đỉnh nên \[x = \widehat {aOn} = \widehat {cOd} = 50^\circ \].
Câu 18:
Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Giả thiết của định lí trên là \[a//b;\;c\, \cap \,a = \left\{ M \right\};\;c\, \cap b = \left\{ N \right\}\].
Câu 19:
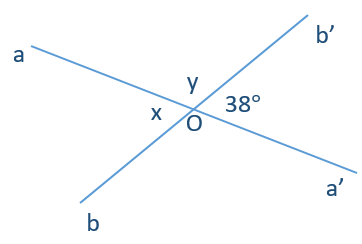
Tìm số đo x và y trong hình vẽ dưới đây:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
+ Góc aOb và góc b’Oa’ là hai góc đối đỉnh nên \[x = \widehat {aOb} = \widehat {b'Oa'} = 38^\circ \]
+ Góc aOb’ và góc b’Oa’ là hai góc kề bù nên
\[\widehat {aOb'} + \widehat {b'Oa'} = 180^\circ \Rightarrow \widehat {aOb'} = 180^\circ - \widehat {b'Oa'} = 180^\circ - 38^\circ = 142^\circ \]
Hay y = 142o
Vậy x = 38° và y = 142°.
Câu 20:
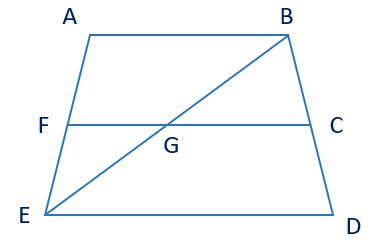
Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.
\[\widehat {ABC}\]và \[\widehat {CDE}\] là hai góc có chung một cạnh BD nhưng không có đỉnh chung;
\[\widehat {BGC}\] và \[\widehat {FGE}\] là hai góc đối đỉnh;
\[\widehat {CGE}\]và \[\widehat {FGB}\] là hai góc đối đỉnh;
\[\widehat {CGE}\] và \[\widehat {EGF}\] là hai góc kề nhau vì có cạnh chung EG và có đỉnh chung.
Câu 21:
Chọn phát biểu đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Giả thiết của định lí là phần cho biết. Kết luận của định lí là điều suy ra.
Câu 22:
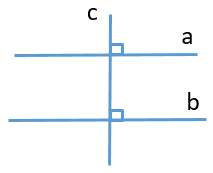
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Hình vẽ minh hoạ cho định lí trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Câu 23:
Viết giả thiết cho định lí sau:
“Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Giả thiết của định lí “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau” là: \[a \ne b;\;a\,//c,\;b\,//c\].
Câu 24:
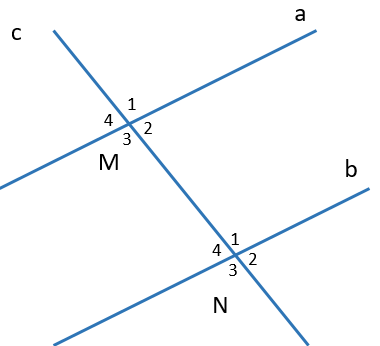
Chọn phát biểu đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
\[\widehat {{M_1}}\] và \[\widehat {{N_1}}\] là hai góc so le trong là phát biểu sai, vì đó là hai góc đồng vị, loại phương án A;
\[\widehat {{M_2}}\] và \[\widehat {{N_2}}\] là hai góc so le ngoài là phát biểu sai, vì đó là hai góc đồng vị, loại phương án B;
\[\widehat {{M_3}}\] và \[\widehat {{N_1}}\] là hai góc đồng vị là phát biểu sai, vì đó là hai góc so le trong, loại phương án C;
\[\widehat {{M_4}}\] và \[\widehat {{N_4}}\] là hai góc đồng vị là phát biểu đúng, chọn phương án D.
Câu 25:
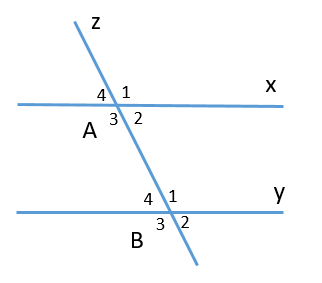
Chọn một cặp góc đồng vị trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
\[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc kề bù, loại phương án A.
\[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc đồng vị là phát biểu đúng, chọn phương án B.
\[\widehat {{A_2}}\] và \[\widehat {{B_4}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{A_2}}\] và \[\widehat {{B_4}}\] là hai góc so le trong, loại phương án C.
\[\widehat {{A_4}}\] và \[\widehat {{A_2}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{A_4}}\] và \[\widehat {{A_2}}\] là hai góc đối đỉnh, loại phương án D.
Câu 26:
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì x, y song song với nhau.
Câu 27:
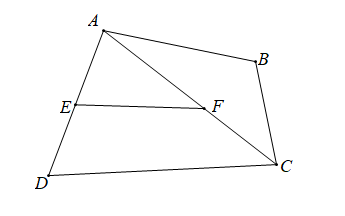
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
\[\widehat {DAC}\] và \[\widehat {AFE}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {DAC}\] và \[\widehat {AFE}\] là hai góc trong một tam giác loại phương án A.
\[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc so le trong là phát biểu đúng, chọn phương án B.
\[\widehat {AFE}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai.
\[\widehat {BAC}\] và \[\widehat {DAC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAC}\] và \[\widehat {DAC}\] có đỉnh chung và có một cạnh chung nên là hai góc kề nhau, do đó loại phương án D.
Câu 28:
Cho hình vẽ. Biết \[\widehat {xOz} = 30^\circ \], Oz là tia phân giác của góc xOy.
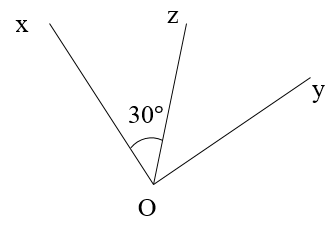
Số đo của góc xOy là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[\widehat {xOz} = \widehat {zOy} = 30^\circ \] (vì Oz là tia phân giác góc xOy)
\[ \Rightarrow \widehat {xOy} = \widehat {xOz} + \widehat {zOy} = 30^\circ + 30^\circ = 60^\circ \]
Vậy \[\widehat {xOy} = 60^\circ \].
Câu 29:
Cho \[\widehat {HOK} = 90^\circ \] và tia OK là tia phân giác của góc HOI. Khi đó góc HOI là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: OK là tia phân giác của góc HOI \[ \Rightarrow \widehat {HOK} = \widehat {KOI} = 90^\circ \]
\[ \Rightarrow \widehat {HOI} = \widehat {HOK} + \widehat {KOI} = 90^\circ + 90^\circ = 180^\circ \]
Vậy góc HOI là góc bẹt.
Câu 30:
Cho \(\widehat {xOy} = 120^\circ \), tia Ot là tia phân giác của góc xOy. Tính số đo góc xOt
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có Ot là tia phân giác góc xOy nên \[\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \].
Vậy \(\widehat {xOt} = 60^\circ .\)
