Có bao nhiêu số nguyên dương y để tập nghiệm của bất phương trình $\left({\log }_{2}x-\sqrt{2}\right)\left({\log }_{2}x-y\right)<0$ chứa tối đa 1000 số nguyên

Cho hàm số y=f(x) có đạo hàm f'(x). Đồ thị của hàm số y=f'(x) như hình vẽ.

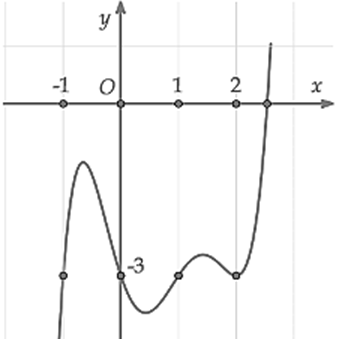
Giá trị lớn nhất của hàm số $g\left(x\right)=f\left(3x\right)+9x$ trên đoạn $\left[-\frac{1}{3};\frac{1}{3}\right]$ là

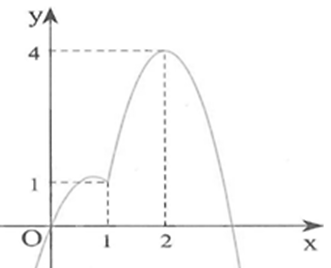
Cho hàm số y=f(x) liên tục trên $\mathrm{ℝ}$ có f(0)=1 và đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số $y=\left|f\left(3x\right)-9x^3-1\right|$ đồng biến trên khoảng:

Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là

Có bao nhiêu cặp số nguyên (x;y) với $1\le x\le 2020$ thỏa mãn $x\left(2^y+y-1\right)=2-{\log }_2{x}^x$

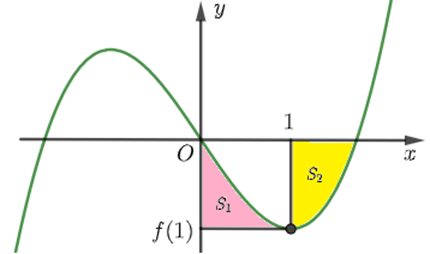
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ, biết f(x) đạt cực tiểu tại điểm x=1 và thỏa mãn $\left[f\left(x\right)+1\right]$ và $\left[f\left(x\right)-1\right]$ lần lượt chia hết cho ${\left(x-1\right)}^2$ và ${\left(x+1\right)}^2$. Gọi $S_1,S_2$ lần lượt là diện tích như trong hình bên. Tính $2S_2+8S_1$

Tập nghiệm S của bất phương trình $5^{1-2\text{x}}>\frac{1}{125}$ là:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, $\angle BAD={60}^0,SO\perp \left(ABCD\right)$ và mặt phẳng (SCD) tạo với đáy một góc ${60}^0$. Tính thế tích khối chóp S.ABCD

Đồ thị hàm số $y=-\frac{x^4}{2}+x^2+\frac{3}{2}$ cắt trục hoành tại mấy điểm?

Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho $MN\perp PQ.$ Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích khối tứ diện MNPQ bằng $36d{m}^3.$ Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).

Cho hàm số f(x) thỏa mãn f(1)=3 và $f\left(x\right)+x{f}^{\text{'}}\left(x\right)=4x+1$ với mọi x>0. Tính f(2)

Tính thể tích của khối nón có chiều cao bằng 4 và độ dài đường sinh bằng 5

Trong không gian tọa độ Oxyz, mặt phẳng chứa trục Oz và đi qua điểm $I\left(1;2;3\right)$ có phương trình là

Số phức nghịch đảo của số phức $z=1+3i$ là

Viết biểu thức $P=\sqrt[3]{x.\sqrt[4]{x}}$(x>0) dưới dạng luỹ thừa với số mũ hữu tỷ

Cho tập hợp $S=\left\{1;2;3;\mathrm{...};17\right\}$ gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên một tập con có 3 phần tử của tập hợp S. Tính xác suất để tập hợp được chọn có tổng các phần tử chia hết cho 3.