Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là
A. 4
B. 3
C. 5
D. 6
 Giải bởi Vietjack
Giải bởi Vietjack
Xét phương trình: 1 + cosx + cos2x + cos3x = 0
\( \Leftrightarrow \)1 + cosx + 2cos2x – 1 + cos3x = 0
\( \Leftrightarrow \)2cos2x + cosx + cos3x = 0
\( \Leftrightarrow \)2cos2x + 2cos2xcosx = 0
\( \Leftrightarrow \)2cosx(cosx + cos2x) = 0
\( \Leftrightarrow 4cosx.cos\frac{{3x}}{2}{\rm{. }}cos\frac{x}{2} = {\rm{ }}0\)
\( \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\cos\frac{{3x}}{2} = 0\\cos\frac{x}{2} = {\rm{ }}0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k\pi \\x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\\x = {\rm{ }}\pi + {\rm{k2}}\pi \end{array} \right.,k \in \mathbb{Z}\)
Điểm A và B biểu diễn nghiệm \(x = \frac{\pi }{2} + k\pi \) trên đường tròn lượng giác.
Điểm C biểu diễn nghiệm \(x = \pi + k2\pi \) trên đường tròn lượng giác.
Điểm D, C và E biểu diễn nghiệm \(x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\) trên đường tròn lượng giác.
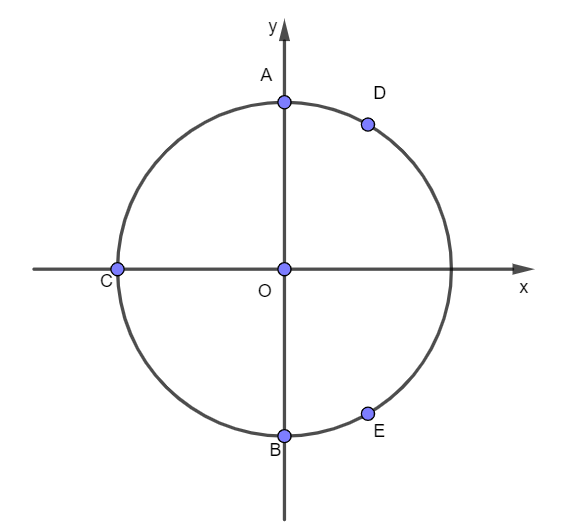
Có tất cả 5 điểm biểu diễn các nghiệm của phương trình đã cho.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm điều kiện cần và đủ của a, b, c để phương trình asinx+bcosx=c có nghiệm
Có bao nhiêu giá trị nguyên m để phương trình có nghiệm thỏa mãn
Cho phương trình . Tính tổng các nghiệm của phương trình trong khoảng (0;2018)
Cho hàm số . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là