Điền số thích hợp vào ô trống:
Một cửa hàng có 58,5kg gạo nếp, số gạo tẻ nhiều hơn gạo nếp 33,8kg. Vậy cửa hàng có tất cả tạ gạo.
 Giải bởi Vietjack
Giải bởi Vietjack
Cửa hàng có số ki-lô-gam gạo tẻ là:
58,5 + 33,8 = 92,3(kg)
Cửa hàng có tất cả số ki-lô-gam gạo là:
58,5 + 92,3 = 150,8(kg)
150,8kg = 1,508 tạ.
Đáp số: 1,508 tạ
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
385,18 trừ đi hiệu của 207,4 và 91, 2891, 28 rồi cộng với 115 được kết quả là:
Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là cm2
Bạn Nam cao 1,57 m, bạn Linh cao 1,53 m, bạn Loan cao 1,49 m.
Chiều cao của bạn cao nhất hơn bạn thấp nhất là bao nhiêu mét?
Tính một cách hợp lí: 89,45 + (−3,28) + 0,55 + (−6,72) ta được kết quả bằng
Bác Đồng của ba thanh gỗ: thanh thứ nhất dài 1,85 m, thanh thứ hai dài hơn thanh thứ nhất 10 cm. Độ dài thanh gỗ thứ ba ngắn hơn tổng độ dài hai thanh gỗ đầu tiên là 1,35 m. Thanh gỗ thứ ba mà bác Đồng đã cưa dài bao nhiêu mét?
Điền số thích hợp vào ô trống:
Cho đường gấp khúc ABCD như hình vẽ:
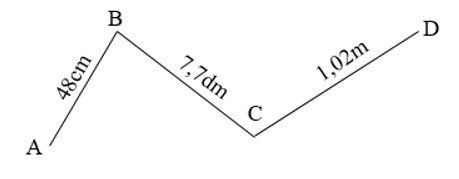
Độ dài đường gấp khúc đó là m.
24,225km + 818m − 67,9hm = ...km.
Số thích hợp điền vào chỗ chấm là:
Điền số thích hợp vào ô trống
Thực hiện phép tính −5,5 + 90,67 ta được kết quả là:
Điền số thích hợp vào ô trống
Kết quả của phép trừ 0,008 − 3,9999 là:
Thực hiện phép tính: (−4,5) + 3,6 + 4,5 + (−3,6) ta được kết quả là:
Điền số thích hợp vào ô trống
Thực hiện phép tính sau: 12,3 + 5,67 ta được kết quả là
Điền số thích hợp vào ô trống
Cho biết một quả chuối nặng 100 g có chứa:
- Chất béo: 0,3 g
- Kali: 0,42 g.
Trong quả chuối đó, khối lượng kali nhiều hơn khối lượng chất béo là g
Điền số thích hợp vào ô trống để tính bằng cách thuận tiện:
245,18 − 81,359 − 17,641 + 113,82
=(245,18 + ) − (81,359 + )
= −
=
Điền số thích hợp vào ô trống
Kết quả của phép tính (−12,3) + (−5,67) là
1. Số đối của số thập phân
Số đối của số thập phân a kí hiệu là ‒a. Ta có: a + (‒a) = 0.
Chú ý: Số đối của số thập phân ‒a là a, tức là ‒(‒a) = a.
Ví dụ 1. Số đối của 1,14 là ‒1,14;
Số đối của số ‒2,568 là 2,568.
2. Phép cộng, phép trừ số thập phân
a) Cộng hai số thập phân
- Cộng hai số thập phân dương: Muốn cộng hai số thập phân dương ta thực hiện quy tắc cộng hai số nguyên dương.
- Cộng hai số thập phân âm: Muốn cộng hai số thập phân âm ta cộng hai số đối của chúng rồi thêm dấu “‒” đằng trước kết quả:
(‒a) + (‒b) = ‒(a + b)
- Cộng hai số thập phân khác dấu, ta làm như sau:
+ Nếu số dương lớn hơn hay bằng số đối của số âm thì lấy số dương trừ đi số đối của số âm.
+ Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ “‒” trước kết quả.
Ví dụ 2. Tính:
a) 1,123 + 2,234;
b) (‒1,058) + (‒3,305);
c) 15,6 + (‒9,58);
d) (‒45,6) + 15,7.
Hướng dẫn giải
a) 1,123 + 2,234 = 3,357;
b) (‒1,058) + (‒3,305) = ‒(1,058 + 3,305) = ‒4,363
c) 15,6 + (‒9,58) = 15,6 ‒ 9,58 = 6,02;
d) (‒45,6) + 15,7 = ‒(45,6 ‒ 15,7) = ‒29,9.
* Tính chất của phép cộng số thập phân:
Giống như phép cộng số nguyên, phép cộng số thập phân có các tính chất giao hoán, kết hợp, cộng với số 0, cộng với số đối.
Ví dụ 3. Tính một cách hợp lí: 34,9 + (–31,5) + 45,81 + (–68,5)
Hướng dẫn giải
34,9 + (–31,5) + 45,81 + (–68,5)
= (34,9 + 45,81) + [(–68,5) + (–31,5)]
= 80 + (–100)
= –(100 – 80)
= – 20.
b) Trừ hai số thập phân
- Muốn trừ hai số thập phân, ta cộng số bị trừ với số đối của số trừ.
a – b = a + (–b)
Ví dụ 4. Tính:
a) (–1,15) – 3,68;
b) (–68,4) – (–45,54);
Hướng dẫn giải
a) (–1,15) – 3,68 = (–1,15) + (–3,68) = –(1,15 + 3,68) = –4,83.
b) (–68,4) – (–45,54) = (–68,4) + 45,54 = –(68,4 – 45,54) = –22,86.
3. Quy tắc dấu ngoặc
- Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.
- Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”:
a ‒ (b + c – d) = a ‒ b ‒ c + d
Ví dụ 5. Tính một cách hợp lí: (–46,75) – (–1,76 + 53,25).
Huớng dẫn giải
(–46,75) – (1,76 + 53,25)
= (–46,75) – 1,76 – 53,25
= (–1,76) + (–46,75) – 53,25
= (–1,76) + [(–46,75) + (–53,25)]
= (–1,76) + (–100)
= –(1,76 + 100)
= –101,76.