Cho hình chóp có đáy là hình thoi cạnh a và . Các mặt phẳng và cùng vuông góc với mặt phẳng đáy . Góc tạo bởi với bằng . Cho là điểm nằm trên cạnh sao cho . Khoảng cách giữa hai đường thẳng và là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
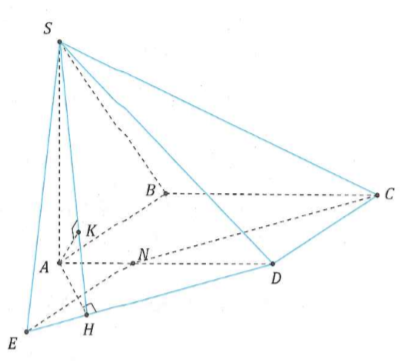
Gọi là điểm thỏa mãn là hình bình hành.
Kẻ .
Ta có .
Mặt khác
.
Vì là hình thoi cạnh a và nên đều có cạnh bằng a.
.
Ta có:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
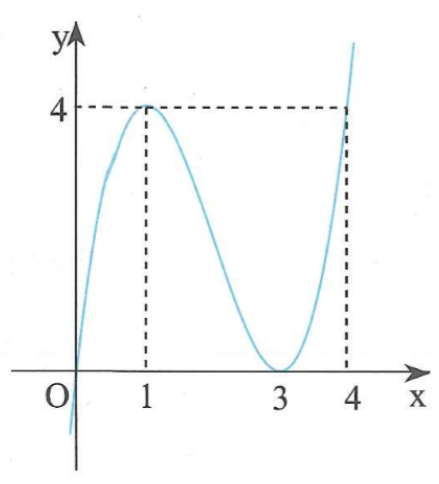
Cho hàm số có đồ thị như hình vẽ bên. Phương trình có tất cả bao nhiêu nghiệm thực phân biệt?
Cho khối chóp có đáy là hình vuông cạnh a. Hai mặt phẳng và cùng vuông góc với đáy. Biết khoảng cách từ S đến mặt phẳng là a. Thể tích khối chóp bằng:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hệ số góc nhỏ nhất là:
Cho hai mặt phẳng . Gọi là góc giữa hai mặt phẳng và thì giá trị đúng của là:
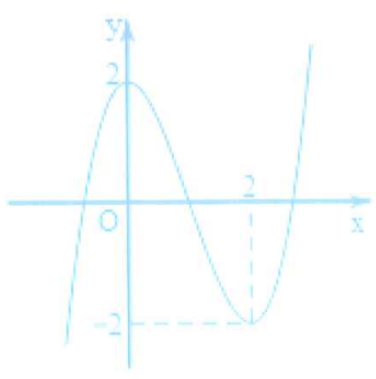
Cho hàm m có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số trên đoạn bằng 4?
Tỉ số diện tích mặt cầu nội tiếp hình lập phương có cạnh bằng 2 và diện tích toàn phần của hình lập phương đó là:
Cho và mặt phẳng . Hình chiếu vuông góc của lên có phương trình là:
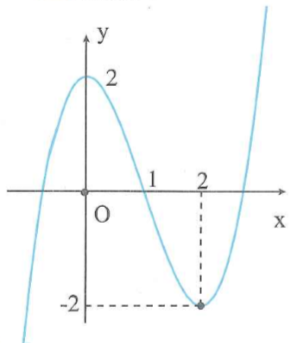
Cho đồ thị hàm số như hình vẽ, hàm số nghịch biến trên khoảng nào trong các khoảng sau đây?
Cho số phức z có . Khi đó, quỹ tích các điểm biểu diễn số phức là:
Cho hình chóp tứ giác đều có các mặt bên là những tam giác đều. Cosin của góc giữa mặt bên và mặt đáy của hình chóp là: