Cho hàm số $y=f\left(x\right)=a{x}^3+b{x}^2+cx+d$ có đồ thị như hình bên. Khẳng định nào sau đây là khẳng định sai?

Cho lăng trụ tam giác ABC.A'B'C' có BB'=a, góc giữa đường thẳng BB' và (ABC) bằng 60°, tam giác ABC vuông tại C và góc $\widehat{BAC}={60}^o.$ Hình chiếu vuông góc của điểm B' lên (ABC) trùng với trọng tâm của $△$ABC . Thể tích của khối tứ diện A'.ABC theo a bằng

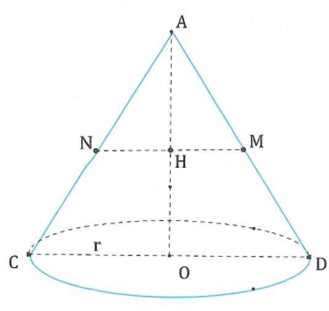
Một hình nón được cắt bởi một mặt phẳng (P) song song với đáy. Mặt phẳng này chia với mặt xung quanh của hình nón thành hai phần có diện tích bằng nhau như hình vẽ. Gọi (N₁) là hình nón có đỉnh A, bán kính đáy HM; (N₂) là hình nón có đỉnh A, bán kính đáy OD. Tỉ số thể tích của khối nón (N₁) và khối nón (N₂) là

Cho parabol $\left(P\right):y=-x^2+2x,$ có đỉnh S và A là giao điểm khác O của (P) và trục hoành. M là điểm di động trên cung nhỏ SA, tiếp tuyến của (P) tại M cắt Ox, Oy tại E, F. Khi đó, tổng diện tích 2 tam giác cong MOF và MAE có giá trị nhỏ nhất bằng

Trong hệ tọa độ Oxyz, cho điểm M(1;2;-4). Khoảng cách từ M đến trục Oz bằng

Cho hình trụ có thể tích bằng $16\mathrm{\pi }{a}^3$, đường kính đáy bằng 4a. Chiều cao của hình trụ bằng

Số giao điểm của đồ thị hàm số $y=x^3-3x+3$ và đường thẳng y=x là

Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có chiều cao bằng 6a và đường chéo 10a. Thể tích khối lăng trụ này là

Cho mặt cầu $\left(S\right):x^2+y^2+z^2-2x+4z+1=0$ và đường thẳng $d:\left\{\begin{array}{l}x=2-t\\ y=t\\ z=m+t\end{array}\right..$ Tổng các giá trị của m để d cắt (S) tại 2 điểm phân biệt A, B sao cho các mặt phẳng tiếp diện của (S) tại A và B vuông góc với nhau

Cho hình lăng trụ ABCD.A'B'C'D' có M là điểm nằm trong tứ giác ABCD sao cho $S_{ABCD}=5S_{ABM}.$ Gọi O' là điểm bất kì nằm trong (A'B'C'D'). Tỉ số thể tích hình chóp O'.ABM và hình lăng trụ ABCD.AB'C'D' bằng

Cho số phức z=2-5i. Khi đó mô đun của $z^{-1}$ là

Cho hình phẳng giới hạn bởi hai đồ thị hàm số $y={\log }_{2}x,y=0,x=4.$ Đường thẳng y=2 chia hình phẳng đó thành 2 hình có diện tích là $S_1>S_2.$ Tỷ lệ thể tích $\frac{S_1-2}{S_2}$ là

Một quả bóng bầu dục có khoảng cách giữa 2 điểm xa nhất bằng 20 cm và cắt quả bóng bằng mặt phẳng trung trực của đoạn thẳng đó thì được đường tròn có diện tích bằng 16$\mathrm{\pi }$(cm²). Thể tích của quả bóng bằng bao nhiêu? (Tính gần đúng đến hai chữ số thập phân)

Cho hình nón có diện tích xung quanh là $S_{xq}=10\pi c{m}^2,$ bán kính đáy R=3cm. Khi đó đường sinh của hình nón là

Tập xác định của hàm số $y={\log }_{2x-1}\left(x^2-3x+2\right)$ là

Nghiệm của phương trình ${10}^{\log 2}=3x+5$ là