Viết số 12 thành tích của các thừa số nguyên tố.
Giải bởi Vietjack
Cách 1. Quan sát và thực hiện lần lượt:
+) Tìm một ước nguyên tố của 12, chẳng hạn là 2.
+) Viết số 12 thành tích của 2 với một thừa số khác: 12 = 2 . 6
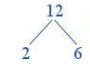
Vẽ hai nhánh từ số 12 cho hai thừa số 2 và 6.
+) Tiếp tục tìm một ước nguyên tố của 6, chẳng hạn là 2.
+) Viết số 6 thành tích của 2 với một thừa số khác: 6 = 2 . 3
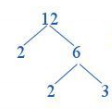
Vẽ tiếp hai nhánh từ số 6 cho hai thừa số 2 và 3.
+) Các thừa số 2 và 3 đều là số nguyên tố nên ta dừng lại.
Lấy tích tất cả các thừa số ở cuối cùng mỗi nhánh, ta có:
Các thừa số trong tích cuối cùng đều là số nguyên tố. Ta nói số 12 đã được phân tích ra thừa số nguyên tố.
Cách 2. Ta có thể viết lại quá trình phân tích số 12 ra thừa số nguyên tố “theo cột dọc” như sau:
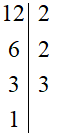
Lấy 12 chia cho ước nguyên tố 2.
Lấy thương là 6 chia tiếp cho ước nguyên tố 2.
Lấy thương 3 chia tiếp cho ước nguyên tố 3
Vậy ta phân tích được: 12 = 2.2.3 = .3
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
a) Biết 400 = . . Hãy viết 800 thành tích các thừa số nguyên tố.
b) Biết 320 = . 5. Hãy viết 3 200 thành tích các thừa số nguyên tố.
Phân tích số 84 ra thừa số nguyên tố rồi tìm tập hợp các ước của nó.
a) Biết 2700 = . . . Hãy viết 270 và 900 thành tích các thừa số nguyên tố.
b) Biết 3600 = . . . Hãy viết 180 và 600 thành tích các thừa số nguyên tố.
Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”
a) Hãy nêu các số nguyên tố nhỏ hơn 30.
b) Tìm một ước nguyên tố của 91.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
