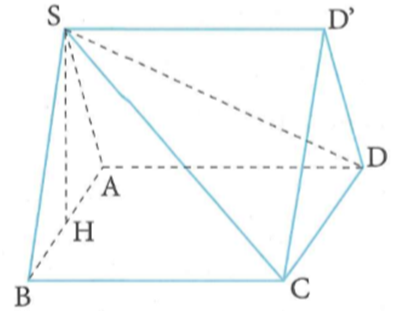
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB,CD thỏa mãn CD=2AB và diện tích bằng 27, đỉnh .A(-1;-1;0) Phương trình đường thẳng chứa cạnh $CD:\frac{x-2}{2}=\frac{y+1}{2}=\frac{z-3}{1}$. Tìm tọa độ điểm D biết $x_B>x_A$?

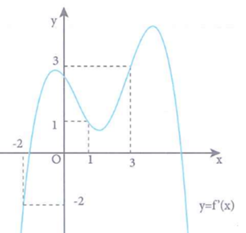
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số $y=g\left(x\right)=f\left(2-x\right)$ đồng biến trên khoảng:

Tìm tập nghiệm S của phương trình $3^x=2$:

Cho hàm số $y=x^3-3x^2+6x+1$ có đồ thị (C). Tiếp tuyến của (C) có hệ số góc nhỏ nhất là bao nhiêu?

Tập nghiệm của bất phương trình ${\log }_{0,5}\left(x-3\right)+1\ge 0$ là:

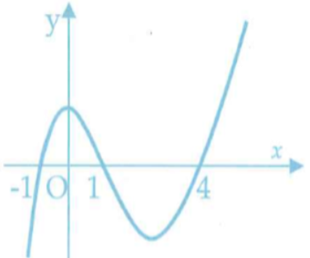
Cho đồ thị của ba hàm số $y=a^x;y=b^x;y=c^x$ như hình vẽ. Mệnh đề nào dưới đây là mệnh đề đúng?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi $\alpha$ là góc tạo bởi đường thẳng SD và mặt phẳng (SBC), với $\alpha <{45}^0$. Tìm giá trị lớn nhất của thể tích khối chóp S.ABCD.

Cho hai số phức $z_1,z_2$ thỏa mãn đồng thời hai điều kiện sau: $\left|z-1\right|=\sqrt{34};\left|z+1+mi\right|=\left|z+m+2i\right|$ (trong đó m là số thực) và sao cho $\left|z_1-z_2\right|$ là lớn nhất. Khi đó giá trị của $\left|z_1+z_2\right|$ bằng:

Cho hàm số y=f(x) xác định trên $ℝ\backslash \left\{-1\right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

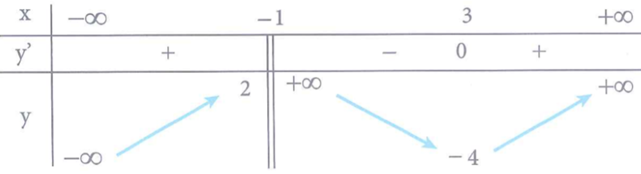
Số nghiệm thực của phương trình 2f(x)-4=0 là:

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, trục hoành và đường thẳng x=4. Thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục  bằng

Số tập hợp con có 5 phần tử của một tập hợp có 10 phần tử là:

Cho hàm số $y=\frac{4x-5}{x+1}$ có đồ thị (H). Gọi $M\left(x_0;y_0\right)$ với $x_0<0$ là một điểm thuộc đồ thị (H) thỏa mãn tổng khoảng cách từ M đến hai đường tiệm cận của (H) bằng 6. Tính giá trị biểu thức $S={\left(x_0+y_0\right)}^2$?

Cho hàm số f(x) liên tục trên đoạn $\left[0;\frac{\pi }{2}\right]$ và $f\left(x\right)+f\left(\frac{\pi }{2}-x\right)=\frac{\cos x}{{\left(1+\sin x\right)}^2},\forall x\in \left[0;\frac{\pi }{2}\right]$. Tính tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}f\left(x\right)dx$

Cho hàm số f(x) xác định trên $ℝ\backslash \left\{-1;2\right\}$, liên tục trên các khoảng xác định của nó và có bảng biến thiên như sau:

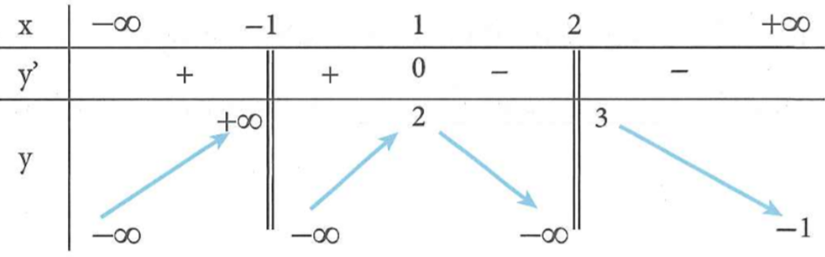
Số đường tiệm cận của đồ thị hàm số $y=\frac{1}{f\left(x\right)-1}$ là:

Biết F(x) là một nguyên hàm của hàm f(x)=sin2x và $F\left(\frac{\pi }{4}\right)=1$. Tính $F\left(\frac{\pi }{6}\right)$?

Cho hàm số f(x) liên tục và có đạo hàm trên $ℝ$. Có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết phương trình $2f\left(x\right)>x^2+m$ đúng với mọi $x\in \left[-2;3\right]$ khi và chỉ khi: