Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;8;2) và mặt cầu (S) có phương trình và điểm . Viết phương trình mặt phẳng (P) qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến (P) lớn nhất. Giả sử là một vectơ pháp tuyến của (P), tính tích m.n.
A. m.n=2
B. m.n=-2
C. m.n=4
D. m.n=-4
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Cách 1:
Mặt cầu (S) có tâm I(5;-3;7) và bán kính .
nên điểm A nằm ngoài mặt cầu.
nên điểm B nằm ngoài mặt cầu.
không thẳng hàng.
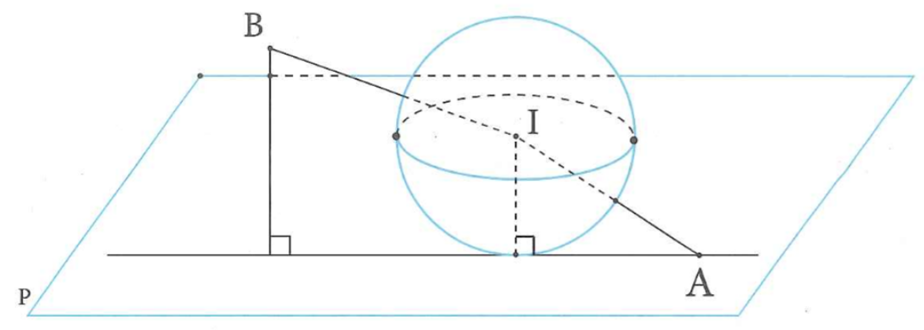
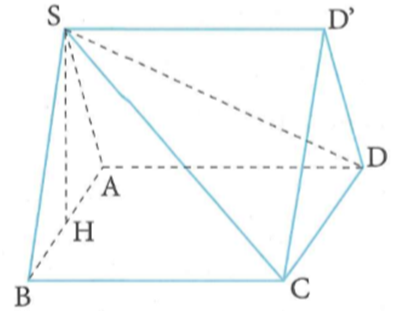
Mặt phẳng (P) qua A và tiếp xúc với (S) nên khi (P) thay đổi thì tập hợp các đường thẳng qua A và tiếp điểm tạo thành hình nón.
Gọi đạt giá trị lớn nhất A,B,I,H đồng phẳng (H là hình chiếu của B lên (P)).
Mặt phẳng (P) qua A và nhận làm vectơ pháp tuyến nên có phương trình .
Mặt phẳng (P) tiếp xúc với .
Ta có: .
Gọi là vectơ pháp tuyến của mặt phẳng (AIB), chọn .
Do .
Thế (2) vào (1) ta được phương trình:
Thay m=-1 vào (2) suy ra: n=4.
Vậy .
Cách 2:
Mặt cầu (S) có tâm I(5;-3;7) và bán kính .
Mặt phẳng (P) qua A và nhận làm vectơ pháp tuyến nên có phương trình .
Mặt phẳng (P) tiếp xúc với (S):
Dấu bằng xảy ra khi .
Vậy m.n=-4.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
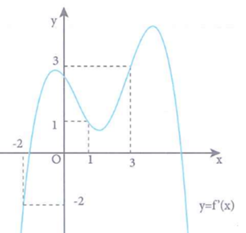
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số đồng biến trên khoảng:
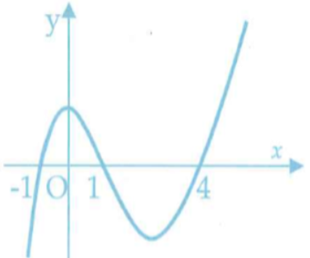
Cho hàm số có đồ thị (C). Tiếp tuyến của (C) có hệ số góc nhỏ nhất là bao nhiêu?
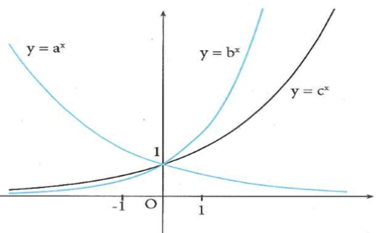
Cho đồ thị của ba hàm số như hình vẽ. Mệnh đề nào dưới đây là mệnh đề đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi là góc tạo bởi đường thẳng SD và mặt phẳng (SBC), với . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCD.
Cho hai số phức thỏa mãn đồng thời hai điều kiện sau: (trong đó m là số thực) và sao cho là lớn nhất. Khi đó giá trị của bằng:
Cho hàm số y=f(x) xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
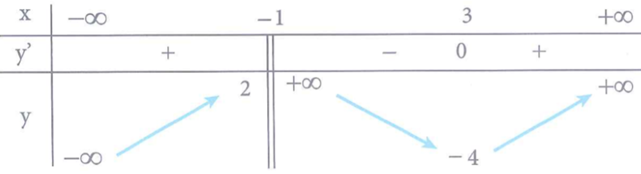
Số nghiệm thực của phương trình 2f(x)-4=0 là:
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số , trục hoành và đường thẳng x=4. Thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục bằng
Cho hàm số có đồ thị (H). Gọi với là một điểm thuộc đồ thị (H) thỏa mãn tổng khoảng cách từ M đến hai đường tiệm cận của (H) bằng 6. Tính giá trị biểu thức ?
Cho hàm số f(x) xác định trên , liên tục trên các khoảng xác định của nó và có bảng biến thiên như sau:
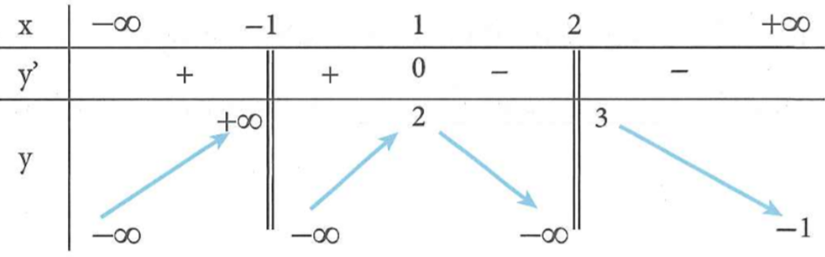
Số đường tiệm cận của đồ thị hàm số là:
Cho hàm số f(x) liên tục và có đạo hàm trên . Có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết phương trình đúng với mọi khi và chỉ khi: