Nêu cách tìm tâm vị tự của hai đường tròn.
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi hai đường tròn là (I1: R1) và (I2; R2).
+ TH1: I1 ≡ I2; khi đó tâm vị tự O ≡ I1 ≡ I2; tỉ số vị tự 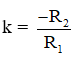
+ TH2: I1 ≠ I2.
Vẽ bán kính I1M bất kì.
Dựng đường kính AB của (I2; R2) sao cho AB // I1M.
MA; MB lần lượt cắt I1I2 tại O1 và O2.
Khi đó O1 và O2 chính là hai tâm vị tự của hai đường tròn.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
a. Hãy kể tên các phép dời hình đã học.
b. Phép đồng dạng có phải là phép vị tự không?
Thế nào là một phép biến hình, phép dời hình, phép đồng dạng? Nêu mối liên hệ giữa phép dời hình và phép đồng dạng.
Hãy nêu một số tính chất đúng đối với phép dời hình mà không đúng với phép đồng dạng.
Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự.
a. Biến A thành chính nó;
b. Biến A thành B;
c. Biến d thành chính nó.
Thế nào là hai hình bằng nhau, hai hình đồng dạng với nhau? Cho ví dụ.