Cho hình thoi ABCD có tâm \(O,\widehat {ADC} = {60^0},AC = 2a\). Lấy điểm S không thuộc (ABCD) sao cho \[SO \bot (ABCD)\] Gọi \[\alpha \] là góc giữa đường thẳng SB và mặt phẳng (ABCD) và \[tan\alpha = \frac{1}{2}\]. Gọi \[\beta \] là góc giữa SC và (ABCD)(ABCD), chọn mệnh đề đúng :
A.\[\sin \beta = \frac{1}{2}\]
B. \[\cot \beta = \frac{{\sqrt 3 }}{2}\]
C. \[\tan \beta = \frac{{\sqrt 3 }}{2}\]
D. \[\beta = {60^0}\]
Giải bởi Vietjack
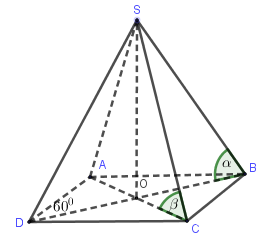
Vì \[SO \bot (ABCD)\;\] nên OB là hình chiếu của SB trên mặt phẳng đáy.
Do đó \[\alpha = \left( {SB,\left( {ABCD} \right)} \right) = \left( {SB,OB} \right) = \widehat {SBO}\] và \[\beta = \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,OC} \right) = \widehat {SCO}\] Hình thoi ABCD có \[AC = 2a,\widehat {ADC} = {60^0} \Rightarrow {\rm{\Delta }}ADC\] đều \[ \Rightarrow AD = 2a\]
Tam giác AOD vuông tại O nên \[OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \Rightarrow OB = a\sqrt 3 \]
Lại có \[\tan \alpha = \frac{1}{2} \Rightarrow \frac{{SO}}{{OB}} = \frac{1}{2} \Rightarrow SO = \frac{1}{2}OB = \frac{1}{2}.a\sqrt 3 = \frac{{a\sqrt 3 }}{2}\] Vậy \[\tan \beta = \tan \widehat {SCO} = \frac{{SO}}{{OC}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{\sqrt 3 }}{2}\]
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, SA vuông góc với mặt phẳng đáy và \(SA = \sqrt {15} a\) (tham khảo hình bên)
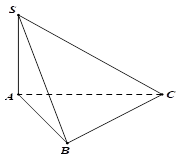
Góc giữa đường thẳng SC và mặt phẳng đáy bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, αα là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Tính \[sin\alpha .\]
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
Cho hình chóp S.ABCD có \[SA \bot (ABCD)\] và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD và I là trung điểm của SC. Khẳng định nào sau đây sai ?
Cho tam giác ABC vuông cân tại A và BC=a.. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm SS sao cho \(SA = \frac{{a\sqrt 6 }}{2}\). Tính số đo góc giữa đường thẳng SA và (ABC)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm \[\Delta ABC\]. Độ dài SG là:
Cho hình chóp S.ABCD, với đáy ABCD là hình bình hành tâm O;AD,SA,AB đôi một vuông góc AD=8,SA=6. (P)là mặt phẳng qua trung điểm của AB và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng?
Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng aa và \[SA \bot (ABCD)\] Biết \(SA = \frac{{a\sqrt 6 }}{3}\). Tính góc giữa SC và (ABCD).
Cho tứ diện ABCD đều. Gọi α là góc giữa AB và mp(BCD). Chọn khẳng định đúng trong các khẳng định sau?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với mp(ABCD). Gọi α là góc giữa BD và mp(SAD). Chọn khẳng định đúng trong các khẳng định sau?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \[SA \bot (ABCD),\;SA = a\sqrt 6 \]. Gọi \[\alpha \] là góc giữa SC và mp(SAB). Chọn khẳng định đúng trong các khẳng định sau?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC=a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB=a. Tính số đo của góc giữa SA và (ABC).
Cho hình lập phương ABCD.A′B′C′D′. Gọi \[\alpha \] là góc giữa AC′ và mp .(A′BCD′). Chọn khẳng định đúng trong các khẳng định sau?
