Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số $y = {x^3} + 3m{x^2} - 3x$

Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$. Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có một góc 120^o là:

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1$ có hai điểm cực trị nằm về hai phía của trục hoành.

Tìm tất cả các giá trị của m để hàm số $y = \frac{{m{x^3}}}{3} - m{x^2} + x - 1$  có cực đại và cực tiểu.

Cho hàm số $y = {x^4} + 2\left( {1 - {m^2}} \right){x^2} + m + 1.$. Tất cả các giá trị của mm để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có diện tích bằng $4\sqrt 2$là

Cho hàm số $f\left( x \right) = \frac{1}{3}{x^3} + m{x^2} + \left( {{m^2} - 4} \right)x + 1$. Có bao nhiêu giá trị nguyên của tham số mm để hàm số $y = f(|x|)\;$ có đúng 3 điểm cực trị?

Tìm tất cả các giá trị của tham số m để hàm số $y = {x^3} - 2m{x^2} + {m^2}x + 2\;$ đạt cực tiểu tại x=1.

Hàm số $f\left( x \right) = \left| {\frac{x}{{{x^2} + 1}} - m} \right|$ (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?

Tìm tất cả các giá trị của tham số m để hàm số $y = - {x^3} - 3{x^2} + mx + 2\;$ có cực đại và cực tiểu?

Cho hàm số $y = {x^4} - 2m{x^2} + 3m + 2.$. Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác đều là:

Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số $y = \mid 3{x^4} - 4{x^3} - 12{x^2} + m\mid \;$ có 5 điểm cực trị?

Tìm m để (Cm) : $y = {x^4} - 2m{x^2} + 2\;$ có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân.

Gọi k là số giá trị nguyên của tham số m để hàm số $y = \frac{1}{3}{x^3} - {x^2} + ({m^2} - 8m + 16)x - 31\;$ có cực trị. Tìm k.

Cho hàm số $y = 2{x^4} - \left( {m + 1} \right){x^2} - 2.$. Tất cả các giá trị của m để hàm số có 1 điểm cực trị là:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm $g\prime (x) = f(x) + m$. Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.

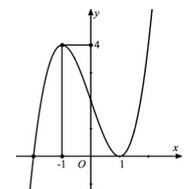
Cho hàm số $y = {x^3} - 3m{x^2} + 4{m^2} - 2$ với m là tham số thực. Tìm giá trị của mm để đồ thị hàm số có hai điểm cực trị A,B sao cho I(1;0) là trung điểm của đoạn thẳng AB.