Xét các số thực dương a và b thỏa mãn \[{\log _3}\left( {1 + ab} \right) = \frac{1}{2} + {\log _3}\left( {b - a} \right)\]. Giá trị nhỏ nhất của biểu thức \[P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}}\] bằng:
 Giải bởi Vietjack
Giải bởi Vietjack
Bước 1: Tìm điều kiện và tìm mối quan hệ giữa a và b từ đẳng thức bài cho.
ĐKXĐ:\(\left\{ {\begin{array}{*{20}{c}}{b - a > 0}\\{a,b > 0}\end{array}} \right.\)
Ta có:
\[\begin{array}{*{20}{l}}{{{\log }_3}\left( {1 + ab} \right) = \frac{1}{2} + {{\log }_3}\left( {b - a} \right)}\\{ \Leftrightarrow {{\log }_3}\left( {1 + ab} \right) - {{\log }_3}\left( {b - a} \right) = \frac{1}{2}}\\{ \Leftrightarrow {{\log }_3}\frac{{1 + ab}}{{b - a}} = \frac{1}{2}}\\{ \Leftrightarrow \frac{{1 + ab}}{{b - a}} = \sqrt 3 }\\{ \Leftrightarrow 1 + ab = \sqrt 3 \left( {b - a} \right)}\\{ \Leftrightarrow \frac{1}{a} + b = \sqrt 3 \left( {\frac{b}{a} - 1} \right)}\end{array}\]
Bước 2: Sử dụng BĐT Cô-si để đánh giá\[\frac{a}{b}\]
Áp dụng BĐT Cô-si ta có\[\frac{1}{a} + b \ge 2\sqrt {\frac{b}{a}} \] nên\[\sqrt 3 \left( {\frac{b}{a} - 1} \right) \ge 2\sqrt {\frac{b}{a}} \Leftrightarrow \sqrt 3 \frac{b}{a} - 2\sqrt {\frac{b}{a}} - \sqrt 3 \ge 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt {\frac{b}{a}} \ge \sqrt 3 }\\{\sqrt {\frac{b}{a}} \le - \frac{1}{{\sqrt 3 }}(Loai)}\end{array}} \right. \Leftrightarrow \sqrt {\frac{b}{a}} \ge \sqrt 3 \Leftrightarrow \frac{b}{a} \ge 3\)
Bước 3: Sử dụng BĐT Cô-si để đánh giá P.
Ta có: \[P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}} = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}}\]
Áp dụng BĐT Cô-si ta có \[1 + {a^2}{b^2} \ge 2\sqrt {{a^2}{b^2}} = 2ab\] nên
\[1 + {a^2} + {b^2} + {a^2}{b^2} \ge {a^2} + {b^2} + 2ab = {\left( {a + b} \right)^2}\]
\[ \Rightarrow P = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}} \ge \frac{{{{\left( {a + b} \right)}^2}}}{{a\left( {a + b} \right)}} = \frac{{a + b}}{a} = 1 + \frac{b}{a} \ge 4\]
Vậy
\[{P_{min}} = 4 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} = b}\\{\frac{b}{a} = 3}\\{a,b > 0,b - a > 0}\end{array}} \right.\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} = 3a}\\{b = 3a}\\{a,b > 0,b - a > 0}\\{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{\sqrt 3 }}}\\{b = \sqrt 3 }\end{array}} \right.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Xét bất phương trình \[\log _2^22x - 2\left( {m + 1} \right){\log _2}x - 2 < 0\]. Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng \[\left( {\sqrt 2 ; + \infty } \right).\]
Giải bất phương trình \[{\log _{\frac{1}{3}}}(x + {9^{500}}) > - 1000\]
Cho \[m = {\log _a}\sqrt {ab} \] với a,b>1 và \[P = \log _a^2b + 54{\log _b}a\]. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là:
Tập nghiệm của bất phương trình \[\log \left( {{x^2} + 25} \right) > \log \left( {10x} \right)\] là:
Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng với mọi y luôn tồn tại không quá 63 số nguyên x thỏa mãn điều kiện \[{\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) \ge {\log _4}\left( {x - y} \right)\]
Tập nghiệm của bất phương trình \[{9^{\log _9^2x}} + {x^{{{\log }_9}x}} \le 18\]là:
Tập hợp nghiệm của bất phương trình \(\)\[{\log _{\frac{1}{3}}}\left( {{x^2} - 2x + 1} \right) < {\log _{\frac{1}{3}}}\left( {x - 1} \right)\] là:
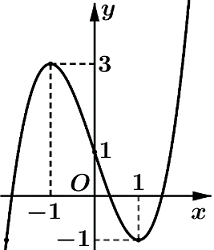
Cho hàm số y=f(x). Hàm số y=f′(x) có đồ thị như hình bên. Biết \[f\left( { - 1} \right) = 1,f( - \frac{1}{e}) = 2.\]. Tìm tất cả các giá trị của m để bất phương trình \[f(x) < ln( - x) + m\;\] nghiệm đúng với mọi \[x \in ( - 1; - \frac{1}{e}).\]
Số nguyên nhỏ nhất thỏa mãn \[{\log _2}\left( {5x - 3} \right) > 5\] là:
Xác định tập nghiệm S của bất phương trình \[\ln {x^2} > \ln \left( {4x - 4} \right)\]
Tập nghiệm của bất phương trình\[{\log _2}\left( {x\sqrt {{x^2} + 2} + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2} \le 1\] là \(\left( { - \sqrt a ; - \sqrt b } \right)\).Khi đó abab bằng
Xét các số thực không âm a,b thỏa mãn \[2a + b \le lo{g_2}\left( {2a + b} \right) + 1\]. Giá trị nhỏ nhất của \[{a^2} + {b^2}\;\] bằng bao nhiêu?
Bất phương trình \[{\log _{\frac{4}{{25}}}}(x + 1) \ge {\log _{\frac{2}{5}}}x\] tương đương với bất phương trình nào dưới đây?
Tập nghiệm của phương trình \[{\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\] là