Bất phương trình logarit
-
453 lượt thi
-
35 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Bất phương trình \[{\log _{\frac{4}{{25}}}}(x + 1) \ge {\log _{\frac{2}{5}}}x\] tương đương với bất phương trình nào dưới đây?
 Xem đáp án
Xem đáp án
Ta có \[{\log _{\frac{4}{{25}}}}\left( {x + 1} \right) = \frac{1}{2}{\log _{\frac{2}{5}}}\left( {x + 1} \right)\]nên bất phương trình đã cho tương đương với:
\[\frac{1}{2}{\log _{\frac{2}{5}}}\left( {x + 1} \right) \ge {\log _{\frac{2}{5}}}x \Leftrightarrow {\log _{\frac{2}{5}}}\left( {x + 1} \right) \ge 2{\log _{\frac{2}{5}}}x\]
Đáp án cần chọn là: C
Câu 2:
Giải bất phương trình \[{\log _2}\left( {3x - 1} \right) \ge 3\]
 Xem đáp án
Xem đáp án
Điều kiện: \[x > \frac{1}{3}\]
BPT\[ \Leftrightarrow 3x - 1 \ge 8 \Leftrightarrow x \ge 3\]
Kết hợp điều kiện ta được\[x \ge 3\]
Đáp án cần chọn là: A
Câu 3:
Giải bất phương trình \[{\log _{\frac{1}{3}}}(x + {9^{500}}) > - 1000\]
 Xem đáp án
Xem đáp án
Điều kiện\[x + {9^{500}} > 0 \Leftrightarrow x > - {9^{500}}\]
Vì \[0 < {\rm{a}} = \frac{1}{3} < 1\]nên
\[\begin{array}{l}{\log _{\frac{1}{3}}}\left( {x + {9^{500}}} \right) > - 1000\\ \Leftrightarrow 0 < x + {9^{500}} < {\left( {\frac{1}{3}} \right)^{ - 1000}}\\ \Leftrightarrow 0 < x + {9^{500}} < {3^{1000}}\\ \Leftrightarrow - {9^{500}} < x < {3^{1000}} - {9^{500}}\\ \Leftrightarrow - {3^{1000}} < x < {3^{1000}} - {3^{1000}}\\ \Leftrightarrow - {3^{1000}} < x < 0\end{array}\]
Đáp án cần chọn là: D
Câu 4:
Số nguyên nhỏ nhất thỏa mãn \[{\log _2}\left( {5x - 3} \right) > 5\] là:
 Xem đáp án
Xem đáp án
Điều kiện:\[x > \frac{3}{5}\]
\[{\log _2}\left( {5x - 3} \right) > 5 \Leftrightarrow 5x - 3 > {2^5} \Leftrightarrow 5x > 35 \Leftrightarrow x > 7\]
Vậy số nguyên nhỏ nhất thỏa mãn bất phương trình là x=8.
Đáp án cần chọn là: B
Câu 5:
Tìm tập nghiệm S của bất phương trình \[{\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right)\]
 Xem đáp án
Xem đáp án
Điều kiện\(\left\{ {\begin{array}{*{20}{c}}{x - 1 > 0}\\{5 - 2x > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 1}\\{x < \frac{5}{2}}\end{array}} \right.\)
\[{\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right) \Leftrightarrow x - 1 < 5 - 2x \Leftrightarrow x < 2\]
Kết hợp với điều kiện suy ra\[S = (1;2)\]
Đáp án cần chọn là: D
Câu 6:
Tìm tất cả các giá trị thực của tham số m để bất phương trình \[4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\]nghiệm đúng với mọi giá trị \[x \in \left[ {1;64} \right]\]
 Xem đáp án
Xem đáp án
Điều kiện : \[x > 0\]\[4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0 \Leftrightarrow 4.{\left( {{{\log }_2}\sqrt x } \right)^2} + 2.{\log _2}\sqrt x \ge - m\](1)
Đặt\[t = {\log _2}\sqrt x \] Khi\[x \in \left[ {1;64} \right] \Rightarrow t \in \left[ {0;3} \right]\]
Ta có bất phương trình\[4{t^2} + 2t \ge - m\]
Xét\[f(t) = 4{t^2} + 2t;f'(t) = 8t + 2 > 0,\forall t \in \left[ {0;3} \right]\]
Để (1) nghiệm đúng với\[\forall t \in \left[ {0;3} \right]\] thì\[\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( t \right) \ge - m\]
\[ \Leftrightarrow f(0) \ge - m \Leftrightarrow 0 \ge - m \Leftrightarrow m \ge 0\]
Đáp án cần chọn là: C
Câu 7:
Tập nghiệm của bất phương trình \[\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\] là:
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}\begin{array}{l}\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1 > 1\end{array}\\{ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) > 0}\end{array}\]
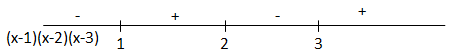
\[ \Rightarrow x \in (1;2) \cup (3; + \infty )\]
Đáp án cần chọn là: A
Câu 8:
Tập nghiệm của bất phương trình \[\log \left( {{x^2} + 25} \right) > \log \left( {10x} \right)\] là:
 Xem đáp án
Xem đáp án
Điều kiện:\[x > 0\]
\[\log ({x^2} + 25) > \log (10x) \Leftrightarrow {x^2} + 25 > 10x \Leftrightarrow {(x - 5)^2} > 0 \Leftrightarrow x \ne 5\]
Tập nghiệm của bất phương trình là:\[(0;5) \cup (5; + \infty )\]
Đáp án cần chọn là: B
Câu 9:
Tập nghiệm của bất phương trình \[({2^{{x^2} - 4}} - 1).\ln {x^2} < 0\]là:
 Xem đáp án
Xem đáp án
Điều kiện:\[x \ne 0\]
\[({2^{{x^2} - 4}} - 1)ln{x^2} < 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{({2^{{x^2} - 4}} - 1) > 0}\\{ln{x^2} < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{({2^{{x^2} - 4}} - 1) < 0}\\{ln{x^2} > 0}\end{array}} \right.}\end{array}} \right.\]</></>
\(\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{2^{{x^2} - 4}} > 1}\\{{x^2} < 1}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{2^{{x^2} - 4}} < 1}\\{{x^2} > 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x^2} - 4 > 0}\\{{x^2} < 1}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x^2} - 4 < 0}\\{{x^2} > 1}\end{array}} \right.}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x > 2;x < - 2}\\{ - 1 < x < 1}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2 < x < 2}\\{x > 1;x < - 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 2 < x < - 1}\\{1 < x < 2}\end{array} \Rightarrow x \in ( - 2; - 1) \cup (1;2)} \right.\end{array}\)
Đáp án cần chọn là: B
Câu 10:
Tập hợp nghiệm của bất phương trình \(\)\[{\log _{\frac{1}{3}}}\left( {{x^2} - 2x + 1} \right) < {\log _{\frac{1}{3}}}\left( {x - 1} \right)\] là:
 Xem đáp án
Xem đáp án
Điều kiện:\(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 2x + 1 > 0}\\{x - 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{(x - 1)}^2} > 0}\\{x - 1 > 0}\end{array}} \right. \Leftrightarrow x > 1\)
\[{\log _{\frac{1}{3}}}({x^2} - 2x + 1) < {\log _{\frac{1}{3}}}(x - 1) \Leftrightarrow {x^2} - 2x + 1 > x - 1 > 0\]</>
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} - 3x + 2 > 0}\\{x - 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(x - 1)(x - 2) > 0}\\{x - 1 > 0}\end{array}} \right. \Leftrightarrow x > 2\)
Đáp án cần chọn là: C
Câu 11:
Tập nghiệm của phương trình \[{\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\] là
 Xem đáp án
Xem đáp án
Điều kiện:\[x > 0;{\log _{\frac{1}{2}}}x > 0 \Rightarrow x < {\left( {\frac{1}{2}} \right)^0} = 1\]
\[{\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1 = {\log _3}3 \Leftrightarrow {\log _{\frac{1}{2}}}x < 3 = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^3}\]
\[ \Leftrightarrow x > {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\] vì\(\frac{1}{2} < 1\)
Đáp án cần chọn là: B
Câu 12:
Nghiệm của bất phương trình \[{\log _2}(x + 1) + {\log _{\frac{1}{2}}}\sqrt {x + 1} \le 0\] là :
 Xem đáp án
Xem đáp án
Điều kiện\[x > - 1\]
Khi đó ta có:
\[\begin{array}{*{20}{l}}{{{\log }_2}(x + 1) - lo{g_2}\sqrt {x + 1} \le 0 \Leftrightarrow {{\log }_2}\frac{{x + 1}}{{\sqrt {x + 1} }} \le 0 \Leftrightarrow \frac{{x + 1}}{{\sqrt {x + 1} }} \le 1}\\{ \Leftrightarrow \frac{{{{(\sqrt {x + 1} )}^2}}}{{\sqrt {x + 1} }} \le 1 \Leftrightarrow \sqrt {x + 1} \le 1 \Leftrightarrow x \le 0}\end{array}\]
Kết hợp với điều kiện ta được:\[ - 1 < x \le 0\]
Đáp án cần chọn là: B
Câu 13:
Giải bất phương trình \[{\log _{0,7}}\left( {{{\log }_6}\frac{{{x^2} + x}}{{x + 4}}} \right) < 0\]
 Xem đáp án
Xem đáp án
\[{\log _{0,7}}({\log _6}\frac{{{x^2} + x}}{{x + 4}}) < 0\]
Đkxđ: \(\left\{ {\begin{array}{*{20}{c}}{{{\log }_6}\frac{{{x^2} + x}}{{x + 4}} > 0}\\{\frac{{{x^2} + x}}{{x + 4}} > 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 4 < x < - 2}\\{x > 2}\end{array}} \right.\left( * \right)\)</>
\(lo{g_6}\frac{{{x^2} + x}}{{x + 4}} > 0,{7^0} = 1 \Leftrightarrow \frac{{{x^2} + x}}{{x + 4}} > 6 \Leftrightarrow \frac{{{x^2} + x}}{{x + 4}} - 6 > 0\)
\( \Leftrightarrow \frac{{{x^2} - 5x - 24}}{{x + 4}} > 0 \Leftrightarrow \frac{{(x - 8)(x + 3)}}{{x + 4}} > 0\)
Xét dấu\[f\left( x \right) = \frac{{(x - 8)(x + 3)}}{{x + 4}}\]
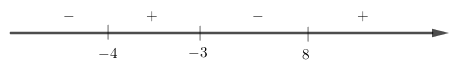
Vậy\[ - 4 < x < - 3\] hoặc\[x > 8\]</>
Kết hợp với điều kiện ta được −4<x<−3 hoặc x>8.</x
Đáp án cần chọn là: A
Câu 14:
Tìm tập hợp nghiệm S của bất phương trình: \[lo{g_{\frac{\pi }{4}}}({x^2} + 1) < lo{g_{\frac{\pi }{4}}}(2x + 4)\]
 Xem đáp án
Xem đáp án
Điều kiện\[x > - 2\]
Bất phương trình \[ \Leftrightarrow {x^2} + 1 > 2x + 4\,(do\,\frac{\pi }{4} < 1)\]
\[ \Leftrightarrow {x^2} - 2x - 3 = (x + 1)(x - 3) > 0\]
Nên x>3 hoặc x<−1.
Kết hợp điều kiện x>−2 ta được x>3 hoặc −2<x<−1.
Đáp án cần chọn là: C
Câu 15:
Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình
\[{\log _m}({2.1^2} + 1 + 3) \le {\log _m}({3.1^2} - 1) \Leftrightarrow {\log _m}6 \le {\log _m}2 \Leftrightarrow 0m < 1\]. Biết rằng x=1x=1 là một nghiệm của bất phương trình.
 Xem đáp án
Xem đáp án
Điều kiện: \(\left\{ {\begin{array}{*{20}{c}}{2{x^2} + x + 3 > 0}\\{3{x^2} - x > 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > \frac{1}{3}}\\{x < 0}\end{array}} \right.\)
Do x=1 là một nghiệm của bất phương trình nên
\[{\log _m}({2.1^2} + 1 + 3) \le {\log _m}({3.1^2} - 1) \Leftrightarrow {\log _m}6 \le {\log _m}2 \Leftrightarrow 0 < m < 1\]
Khi đó, ta có:
\[\begin{array}{l}{\log _m}(2{x^2} + x + 3) \le {\log _m}(3{x^2} - x)\\ \Leftrightarrow 2{x^2} + x + 3 \ge 3{x^2} - x \Leftrightarrow {x^2} - 2x - 3 \le 0 \Leftrightarrow - 1 \le x \le 3\end{array}\]
Kết hợp với điều kiện xác định ta có nghiệm của bpt là :\[S = \left[ { - 1;0} \right) \cup \left( {\frac{1}{3};3} \right)\]
Đáp án cần chọn là: C
Câu 16:
Xác định tập nghiệm S của bất phương trình \[\ln {x^2} > \ln \left( {4x - 4} \right)\]
 Xem đáp án
Xem đáp án
Điều kiện\[x > 1\]
\[\begin{array}{l}\ln {x^2} > \ln \left( {4x - 4} \right)\\ \Leftrightarrow {x^2} > 4x - 4\, \Leftrightarrow {(x - 2)^2} > 0 \Leftrightarrow x \ne 2\\S = \left( {1; + \infty } \right) \setminus \left\{ 2 \right\}\end{array}\]
Đáp án cần chọn là: A
Câu 17:
Tìm tập nghiệm S của bất phương trình \[{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) > {\log _2}\left( {{x^2} - x} \right) - 1\]
 Xem đáp án
Xem đáp án
Thử giá trị \[x = 3:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 < 0\] Loại đáp án A
Thử giá trị \[x = 2:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 = 0\]Loại đáp án D
Thử giá trị x=0,5: MATH ERROR: Loại đáp án C
Đáp án cần chọn là: B
Câu 18:
Tập nghiệm của phương trình \[{\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\] là
 Xem đáp án
Xem đáp án
Điều kiện: \[x > 0;{\log _{\frac{1}{2}}}x > 0 \Rightarrow x < {\left( {\frac{1}{2}} \right)^0} = 1\]
\[{\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1 = {\log _3}3 \Leftrightarrow {\log _{\frac{1}{2}}}x < 3 = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^3}\]
\[ \Leftrightarrow x > {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\] vì \(\frac{1}{2} < 1\)
Đáp án cần chọn là: B
Câu 19:
Giải bất phương trình: \[\log _2^2x - 4033{\log _2}x + 4066272 \le 0\]
 Xem đáp án
Xem đáp án
Điều kiện: \[x > 0\]
Đặt \[t = {\log _2}x\]
BPT\[ \Leftrightarrow {t^2} - 4033t + 4066272 \le 0\]
\[\begin{array}{l} \Leftrightarrow 2016 \le t \le 2017\\2016 \le {\log _2}x \le 2017\\ \Leftrightarrow {2^{2016}} \le x \le {2^{2017}}\end{array}\]
Đáp án cần chọn là: C
Câu 20:
Tập nghiệm của bất phương trình \[{\log _3}x \le {\log _{\frac{1}{3}}}(2x)\] là nửa khoảng \[(a;b]\]. Giá trị của \[{a^2} + {b^2}\;\] bằng
 Xem đáp án
Xem đáp án
Điều kiện:\[x > 0\]
\[{\log _3}x \le {\log _{\frac{1}{3}}}(2x) \Leftrightarrow {\log _3}x \le - {\log _3}(2x)\]
\[ \Leftrightarrow {\log _3}x + {\log _3}(2x) \le 0\]
\[ \Leftrightarrow {\log _3}(2{x^2}) \le 0\]
\[ \Leftrightarrow 2{x^2} \le 1\]
\[ \Leftrightarrow - \frac{{\sqrt 2 }}{2} \le x \le \frac{{\sqrt 2 }}{2}\]
Kết hợp với x>0 ta được\[0 < x \le \frac{{\sqrt 2 }}{2}\]
Do đó\(\left\{ {\begin{array}{*{20}{c}}{a = 0}\\{b = \frac{{\sqrt 2 }}{2}}\end{array}} \right. \Rightarrow {a^2} + {b^2} = \frac{1}{2}\)
Đáp án cần chọn là: C
Câu 21:
Tập nghiệm của bất phương trình \[2017{\log _2}x \le {4^{{{\log }_2}9}}\]là
 Xem đáp án
Xem đáp án
\[2017{\log _2}x \le {9^{{{\log }_2}4}} = 81\]
\[ \Leftrightarrow {\log _2}x = \frac{{81}}{{2017}} = > 0 < x \le \sqrt[{2017}]{{{2^{81}}}}\]
Đáp án cần chọn là: B
Câu 22:
Tập nghiệm của bất phương trình\[{\log _2}\left( {x\sqrt {{x^2} + 2} + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2} \le 1\] là \(\left( { - \sqrt a ; - \sqrt b } \right)\).Khi đó abab bằng
 Xem đáp án
Xem đáp án
Điều kiện :
\[x\sqrt {{x^2} + 2} + 4 - {x^2} > 0 \Leftrightarrow x\left( {\sqrt {{x^2} + 2} - x} \right) + 4 > 0 \Leftrightarrow x.\frac{2}{{\sqrt {{x^2} + 2} + x}} + 4 > 0\]
\[ \Leftrightarrow \frac{{2x}}{{\sqrt {{x^2} + 2} + x}} + \frac{{4\left( {\sqrt {{x^2} + 2} + x} \right)}}{{\sqrt {{x^2} + 2} + x}} > 0 \Rightarrow 6x + 4\sqrt {{x^2} + 2} > 0\] (vì \[\sqrt {{x^2} + 2} > x;\,\forall x\])
\[ \Leftrightarrow 2\sqrt {{x^2} + 2} > - 3x \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3x < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 3x \ge 0}\\{4({x^2} + 2) > {{( - 3x)}^2}}\end{array}} \right.}\end{array}} \right.\]</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 0}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 0}\\{5{x^2} < 8}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 0}\\{ - \frac{{\sqrt {40} }}{5} < x \le 0}\end{array}} \right.\)
Khi đó ta có\[{\log _2}\left( {x\sqrt {{x^2} + 2} + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2} \le 1\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow {{\log }_2}\left( {x\left( {\sqrt {{x^2} + 2} - x} \right) + 4} \right) + 2x + \sqrt {{x^2} + 2} \le 1}\\{ \Leftrightarrow {{\log }_2}\left( {\frac{{2x}}{{\sqrt {{x^2} + 2} + x}} + 4} \right) + 2x + \sqrt {{x^2} + 2} \le 1}\\{ \Leftrightarrow {{\log }_2}\left( {\frac{{6x + 4\sqrt {{x^2} + 2} }}{{\sqrt {{x^2} + 2} + x}}} \right) + 2x + \sqrt {{x^2} + 2} \le 1}\end{array}\]
\[\begin{array}{l} \Leftrightarrow lo{g_2}(6x + 4\sqrt {{x^2} + 2} ) - lo{g_2}(\sqrt {{x^2} + 2 + x} ) + 2x + \sqrt {{x^2} + 2} \le 1\\ \Leftrightarrow lo{g_2}[2(3x + 2\sqrt {{x^2} + 2} )] - lo{g_2}(\sqrt {{x^2} + 2} + x) + 2x + \sqrt {{x^2} + 2} \le 1\\ \Leftrightarrow lo{g_2}2 + lo{g_2}(3x + 2\sqrt {{x^2} + 2} ) - lo{g_2}(\sqrt {{x^2} + 2} + x) + 2x + \sqrt {{x^2} + 2} \le 1\\ \Leftrightarrow 1 + lo{g_2}(3x + 2\sqrt {{x^2} + 2} ) - lo{g_2}(\sqrt {{x^2} + 2} + x) + 2x + \sqrt {{x^2} + 2} \le 1\\ \Leftrightarrow lo{g_2}(3x + 2\sqrt {{x^2} + 2} ) + 3x + 2\sqrt {{x^2} + 2} \le lo{g_2}(\sqrt {{x^2} + 2} + x) + x + \sqrt {{x^2} + 2} ( * )\end{array}\]
Xét hàm số \[f\left( t \right) = t + {\log _2}t\,\] với t>0 ta có \[f'\left( t \right) = 1 + \frac{1}{{t.\ln 2}} > 0;\,\forall t > 0\] nên f(t) là hàm đồng biến trên\[\left( {0; + \infty } \right)\]Từ đó
\[\begin{array}{l}( * ) \Leftrightarrow f(3x + 2\sqrt {{x^2} + 2} ) \le f(\sqrt {{x^2} + 2} + x)\\ \Leftrightarrow 3x + 2\sqrt {{x^2} + 2} \le \sqrt {{x^2} + 2} + x\\ \Leftrightarrow \sqrt {{x^2} + 2} \le - 2x\end{array}\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2x \ge 0}\\{{x^2} + 2 \le 4{x^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \le 0}\\{3{x^2} \ge 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \le 0}\\{\left[ {\begin{array}{*{20}{c}}{x \ge \frac{{\sqrt 6 }}{3}}\\{x \le - \frac{{\sqrt 6 }}{3}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow x \le - \frac{{\sqrt 6 }}{3}\)
Kết hợp điều kiện \(\left[ {\begin{array}{*{20}{c}}{x > 0}\\{ - \frac{{\sqrt {40} }}{5} < x \le 0}\end{array}} \right.\) ta có\[ - \frac{{\sqrt {40} }}{5} < x \le - \frac{{\sqrt 6 }}{3}\] hay\[ - \sqrt {\frac{8}{5}} < x \le - \sqrt {\frac{2}{3}} \]
Tập nghiệm bất phương trình\[S = \left( { - \sqrt {\frac{8}{5}} ; - \sqrt {\frac{2}{3}} } \right]\] nên\[a = \frac{8}{5};b = \frac{2}{3} \Rightarrow a.b = \frac{8}{5}.\frac{2}{3} = \frac{{16}}{{15}}.\]
Đáp án cần chọn là: D
Câu 23:
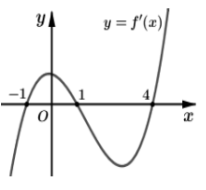
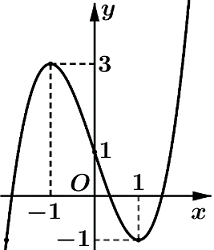
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) và có đồ thị f′(x) như hình vẽ bên. Bất phương trình \[{\log _5}\left[ {f\left( x \right) + m + 2} \right] + f\left( x \right) > 4 - m\] đúng với mọi \[x \in \left( { - 1;4} \right)\;\] khi và chỉ khi
 Xem đáp án
Xem đáp án
ĐK : \[f\left( x \right) + m + 2 > 0\]
Ta có\[{\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) > 4 - m\]
\[ \Leftrightarrow {\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) + m + 2 > 6\left( * \right)\]
Xét hàm số \[y = {\log _5}t + t\,\,\,\left( {t > 0} \right)\] có\[y' = \frac{1}{{t.\ln 5}} + 1 > 0\] với t>0
Nên hàm số\[y = {\log _5}t + t\] đồng biến trên\[\left( {0; + \infty } \right)\] lại có\[y\left( 5 \right) = {\log _5}5 + 5 = 6\]
Nên từ (*) suy ra
\[y\left( {f\left( x \right) + m + 2} \right) > y\left( 5 \right) \Leftrightarrow f\left( x \right) + m + 2 > 5 \Leftrightarrow f\left( x \right) > 3 - m\] (1)
Từ hình vẽ ta có BBT của hàm số f(x) như sau
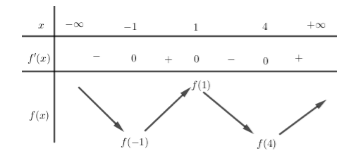
Từ hình vẽ ta có\[\mathop \smallint \limits_{ - 1}^1 \left| {f'\left( x \right)} \right|dx < \mathop \smallint \limits_1^4 \left| {f'\left( x \right)} \right|dx \Leftrightarrow \mathop \smallint \limits_{ - 1}^1 f'\left( x \right)dx < - \mathop \smallint \limits_1^4 f'\left( x \right)dx\]
\[ \Leftrightarrow f(x)|_{ - 1}^1 < - f(x)|_1^4 \Leftrightarrow f(1) - f( - 1) < f(1) - f(4)\,\,\,\,\;\left( 2 \right)\]
Từ (1) ; (2) và BBT ta thấy để phương trình đã cho đúng với \[x \in \left( { - 1;4} \right)\] suy ra\[3 - m \le f\left( 4 \right) \Leftrightarrow m \ge 3 - f\left( 4 \right).\]
Đáp án cần chọn là: D
Câu 24:
Cho phương trình \[{\log _7}\left( {{x^2} + 2x + 2} \right) + 1 > {\log _7}\left( {{x^2} + 6x + 5 + m} \right)\]. Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập nghiệm chứa khoảng (1;3)?
 Xem đáp án
Xem đáp án
ĐK:\[{x^2} + 6x + 5 + m > 0.\]
\[\begin{array}{*{20}{l}}{{{\log }_7}\left( {{x^2} + 2x + 2} \right) + 1 > {{\log }_7}\left( {{x^2} + 6x + 5 + m} \right)}\\{ \Leftrightarrow {{\log }_7}7\left( {{x^2} + 2x + 2} \right) > {{\log }_7}\left( {{x^2} + 6x + 5 + m} \right)}\\{ \Leftrightarrow 7\left( {{x^2} + 2x + 2} \right) > {x^2} + 6x + 5 + m}\\{ \Leftrightarrow 7{x^2} + 14x + 14 - {x^2} - 6x - 5 - m > 0}\\{ \Leftrightarrow 6{x^2} + 8x + 9 - m > 0}\end{array}\]
Bất phương trình đã cho có tập nghiệm chứa (1;3)
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} + 6x + 5 + m > 0,\forall x \in (1;3)}\\{6{x^2} + 8x + 9 - m > 0,\forall x \in (1;3)}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > - {x^2} - 6x - 5,\forall x \in (1;3)}\\{m < 6{x^2} + 8x + 9,\forall x \in (1;3)}\end{array}} \right.\left( * \right)\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ge \mathop {max}\limits_{[1;3]} f(x)}\\{m \le \mathop {min}\limits_{[1;3]} g(x)}\end{array}} \right.\end{array}\)
với\[f\left( x \right) = - {x^2} - 6x - 5\] và\[g\left( x \right) = 6{x^2} + 8x + 9\]
Ta có:\[f'\left( x \right) = - 2x - 6 = 0 \Leftrightarrow x = - 3 \notin \left( {1;3} \right)\] và\[f'\left( x \right) < 0,\forall x \in \left( {1;3} \right)\] nên hàm số\[y = f\left( x \right)\] nghịch biến trên \[\left( {1;3} \right)\]
\[ \Rightarrow \mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 1 \right) = - 12 \Rightarrow m \ge - 12\]
\[g'\left( x \right) = 12x + 8 = 0 \Leftrightarrow x = - \frac{2}{3} \notin \left( {1;3} \right)\] và \[g'\left( x \right) > 0,\forall x \in \left( {1;3} \right)\] nên hàm số\[y = g\left( x \right)\] đồng biến trên (1;3)
\[ \Rightarrow \mathop {\min }\limits_{\left[ {1;3} \right]} g\left( x \right) = g\left( 1 \right) = 23 \Rightarrow m \le 23\]
Vậy\[ - 12 \le m \le 23\]
Mà\[m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 12; - 11;...;23} \right\}\] hay có\[23 - \left( { - 12} \right) + 1 = 36\] giá trị.
Đáp án cần chọn là: A
Câu 25:
Tập nghiệm của bất phương trình \[{9^{\log _9^2x}} + {x^{{{\log }_9}x}} \le 18\]là:
 Xem đáp án
Xem đáp án
ĐKXĐ: x>0.
Ta có:
\[\begin{array}{*{20}{l}}{{9^{\log _9^2x}} + {x^{{{\log }_9}x}} \le 18}\\{ \Leftrightarrow {9^{{{\log }_9}x.{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18}\\{ \Leftrightarrow {{\left( {{9^{{{\log }_9}x}}} \right)}^{{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18}\\{ \Leftrightarrow {x^{{{\log }_9}x}} + {x^{{{\log }_9}x}} \le 18}\\{ \Leftrightarrow 2.{x^{{{\log }_9}x}} \le 18}\\{ \Leftrightarrow {x^{{{\log }_9}x}} \le 9}\end{array}\]
Lấy logarit cơ số 9 cả 2 vế bất phương trình ta được:
\[\begin{array}{*{20}{l}}{{{\log }_9}\left( {{x^{{{\log }_9}x}}} \right) \le {{\log }_9}9}\\{ \Leftrightarrow {{\log }_9}x.{{\log }_9}x \le 1}\\{ \Leftrightarrow \log _9^2x \le 1}\\{ \Leftrightarrow - 1 \le {{\log }_9}x \le 1}\\{ \Leftrightarrow \frac{1}{9} \le x \le 9}\end{array}\]
Kết hợp điều kiện xác định ta có\[x \in \left[ {\frac{1}{9};9} \right]\]
Vậy tập nghiệm của bất phương trình là: \[S = \left[ {\frac{1}{9};9} \right]\]Đáp án cần chọn là: B
Câu 26:
Cho hàm số y=f(x). Hàm số y=f′(x) có đồ thị như hình bên. Biết \[f\left( { - 1} \right) = 1,f( - \frac{1}{e}) = 2.\]. Tìm tất cả các giá trị của m để bất phương trình \[f(x) < ln( - x) + m\;\] nghiệm đúng với mọi \[x \in ( - 1; - \frac{1}{e}).\]
 Xem đáp án
Xem đáp án
ĐKXĐ: \[ - x > 0 \Leftrightarrow x < 0\]
Ta có: \[f\left( x \right) < \ln \left( { - x} \right) + m \Leftrightarrow m > f\left( x \right) - \ln \left( { - x} \right)\left( * \right)\]</>
Xét hàm số \[g\left( x \right) = f\left( x \right) - \ln \left( { - x} \right)\] trên khoảng \[\left( { - 1; - \frac{1}{e}} \right)\] có:
\[\,g'\left( x \right) = f'\left( x \right) - \frac{{ - 1}}{{ - x}} = f'\left( x \right) - \frac{1}{x}\]
Ta biểu diễn đồ thị hàm số\[y = \frac{1}{x}\] (nét màu đỏ) trên hình vẽ như sau:
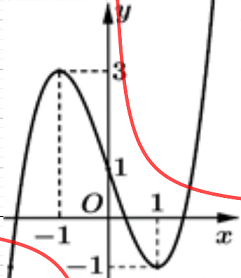
Quan sát đồ thị hàm số ta thấy
\[\,g'\left( x \right) = f'\left( x \right) - \frac{1}{x} > 0,\,\,\forall x \in \left( { - 1; - \frac{1}{e}} \right) \Rightarrow \] Hàm số\[y = g\left( x \right)\] đồng biến trên\[\left( { - 1; - \frac{1}{e}} \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{g( - 1) = f( - 1) - ln(1) = 1}\\{g( - \frac{1}{e}) = f( - \frac{1}{e}) - ln\frac{1}{e} = 2 + 1 = 3}\end{array}} \right.\)
Để (*) nghiệm đúng với mọi\[x \in \left( { - 1; - \frac{1}{e}} \right)\] thì \[ \Leftrightarrow m \ge \mathop {max}\limits_{\left[ { - 1; - \frac{1}{e}} \right]} g\left( x \right) \Leftrightarrow m \ge 3.\]
Đáp án cần chọn là: B
Câu 27:
Xét các số thực không âm a,b thỏa mãn \[2a + b \le lo{g_2}\left( {2a + b} \right) + 1\]. Giá trị nhỏ nhất của \[{a^2} + {b^2}\;\] bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Bước 1: Đặt\[t = 2a + b\;\left( {t \ge 0} \right)\] đưa bất phương trình về dạng\[f\left( t \right) \ge 0\]
Đặt\[t = 2a + b\;\left( {t \ge 0} \right)\] ta có giả thiết đã cho tương đương với\[f\left( t \right) = {\log _2}t - t + 1 \ge 0\]
Ta có\[f'\left( t \right) = \frac{1}{{t\ln 2}} - 1 > 0 \Leftrightarrow t < \frac{1}{{\ln 2}}\] Hàm số đồng biến trên\[\left( {0;\frac{1}{{\ln 2}}} \right)\]
Bước 2: Chứng minh\[t \ge 1\]
Ta chứng minh\[t \ge 1\]
Thật vậy, giả sử t<1 thì \[f\left( t \right) < f\left( 1 \right) = 0\] (mâu thuẫn)
Vậy \[2a + b \ge 1\]
Áp dụng BĐT Cauchy – Schwarz ta có
\[\begin{array}{*{20}{l}}{{{\left( {2a + b} \right)}^2} \le \left( {{2^2} + {1^2}} \right)\left( {{a^2} + {b^2}} \right) = 5\left( {{a^2} + {b^2}} \right)}\\{ \Rightarrow {a^2} + {b^2} \ge \frac{{{{\left( {2a + b} \right)}^2}}}{5} \ge \frac{1}{5}}\end{array}\]
Dấu bằng xảy ra\(\left\{ {\begin{array}{*{20}{c}}{2a + b = 1}\\{\frac{a}{2} = \frac{b}{1}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{2}{5}}\\{b = \frac{1}{5}}\end{array}} \right.\)
Câu 28:
Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng với mọi y luôn tồn tại không quá 63 số nguyên x thỏa mãn điều kiện \[{\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) \ge {\log _4}\left( {x - y} \right)\]
 Xem đáp án
Xem đáp án
Bước 1: Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] và tìm điều kiện xác định.
Đặt\[f\left( x \right) = {\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) - {\log _4}\left( {x - y} \right)\] (coi yy là tham số).
Điều kiện xác định của f(x) là:
\(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} > 0}\\{{y^2} + y + 64 > 0}\\{x - y > 0}\end{array}} \right.\)
Do x,y nguyên nên\[x > y \ge - {y^2}\] Cũng vì x,y nguyên nên ta chỉ xét f(x) trên nửa khoảng \[\left[ {y + 1; + \infty } \right)\]
Bước 2: Xét hàm số trên\[\left[ {y + 1; + \infty } \right)\]
Ta có:
\[f'\left( x \right) = \frac{1}{{\left( {x + {y^2}} \right)\ln 2020}} - \frac{1}{{\left( {x - y} \right)\ln 2021}} - \frac{1}{{\left( {x - y} \right)\ln 4}} < 0,\;\forall x \ge y + 1\]
Bước 3: Lập bảng biến thiên
Ta có bảng biến thiên của hàm số f(x):
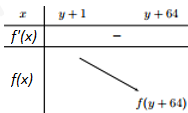
Bước 4: Tìm y nguyên \[f\left( {y + 64} \right) < 0\]
Yêu cầu bài toán trở thành:
\[f\left( {y + 64} \right) < 0\]
\[ \Leftrightarrow {\log _{2020}}\left( {{y^2} + y + 64} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) < {\log _4}64\]
\[ \Leftrightarrow {\log _{2021}}\left( {{y^2} + y + 64} \right)\left( {{{\log }_{2020}}2021 + 1} \right) < 3\]
\[ \Leftrightarrow {y^2} + y + 64 - {2021^{\frac{3}{{{{\log }_{2020}}2021 + 1}}}} < 0\]
\[ \Leftrightarrow - 301,76 < y < 300,76\]
Mà y nguyên nên\[y \in \left\{ { - 301; - 300; \ldots ;299;300} \right\}\]
Vậy có 602 giá trị nguyên của yy thỏa mãn yêu cầu.
Câu 29:
Xét bất phương trình \[\log _2^22x - 2\left( {m + 1} \right){\log _2}x - 2 < 0\]. Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng \[\left( {\sqrt 2 ; + \infty } \right).\]
 Xem đáp án
Xem đáp án
Điều kiện: x>0
\[\log _2^22x - 2\left( {m + 1} \right){\log _2}x - 2 < 0\]
\[ \Leftrightarrow {\left( {1 + {{\log }_2}x} \right)^2} - 2\left( {m + 1} \right){\log _2}x - 2 < 0\left( 1 \right)\]
Đặt \[t = {\log _2}x\]Vì\[x > \sqrt 2 \]nên\[{\log _2}x > {\log _2}\sqrt 2 = \frac{1}{2}\]
Do đó\[t \in \left( {\frac{1}{2}; + \infty } \right)\]
(1) thành\[{\left( {1 + t} \right)^2} - 2\left( {m + 1} \right)t - 2 < 0 \Leftrightarrow {t^2} - 2mt - 1 < 0\left( 2 \right)\]
Yêu cầu bài toán tương đương tìm m để bpt (2) có nghiệm thuộc\[\left( {\frac{1}{2}; + \infty } \right)\]
Xét bất phương trình (2) có: \[{\rm{\Delta '}} = {m^2} + 1 > 0,\forall m \in \mathbb{R}\]
\[f\left( t \right) = {t^2} - 2mt - 1 = 0\]có ac<0 nên f(t) luôn có 2 nghiệm phân biệt\[{t_1} < 0 < {t_2}\]nên tập nghiệm của (2) là\[({t_1};{t_2})\]
Khi đó cần\[\frac{1}{2} < {t_2} \Leftrightarrow m + \sqrt {{m^2} + 1} > \frac{1}{2} \Leftrightarrow m > - \frac{3}{4}\]
Đáp án cần chọn là: C
Câu 30:
Cho \[m = {\log _a}\sqrt {ab} \] với a,b>1 và \[P = \log _a^2b + 54{\log _b}a\]. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là:
 Xem đáp án
Xem đáp án
Ta có \[P = \log _a^2b + 54{\log _b}a = \log _a^2b + \frac{{54}}{{{{\log }_a}b}}\]
Đặt\[t = {\log _a}b\] thì \[P = {t^2} + \frac{{54}}{t}\]
Vì a,b>1 nên\[t = {\log _a}b > 0\]
Áp dụng bất đẳng thức Cô – si ta có
\[P = {t^2} + \frac{{54}}{t} = {t^2} + \frac{{27}}{t} + \frac{{27}}{t} \ge 3\sqrt[3]{{{{27}^2}}} = 27.\]
Đẳng thức xảy ra khi và chỉ khi\[{t^2} = \frac{{27}}{t} \Leftrightarrow t = 3.\]
Ta có\[m = {\log _a}\sqrt {ab} = \frac{1}{2}{\log _a}\left( {ab} \right) = \frac{1}{2}\left( {1 + {{\log }_a}b} \right) = \frac{1}{2}\left( {1 + t} \right) = \frac{1}{2}\left( {1 + 3} \right) = 2\]Đáp án cần chọn là: A
Câu 31:
Tập nghiệm của bất phương trình \[{\left( {\sqrt 5 - 2} \right)^{\frac{{2x}}{{x - 1}}}} \le {\left( {\sqrt 5 + 2} \right)^x}\] là:
 Xem đáp án
Xem đáp án
\[{\left( {\sqrt 5 - 2} \right)^{\frac{{2x}}{{x - 1}}}} \le {\left( {\sqrt 5 + 2} \right)^x} \Leftrightarrow {\left( {\sqrt 5 + 2} \right)^{\frac{{ - 2x}}{{x - 1}}}} \le {\left( {\sqrt 5 + 2} \right)^x} \Leftrightarrow - \frac{{2x}}{{x - 1}} \le x\]
\[ \Leftrightarrow \frac{{2x}}{{x - 1}} + x \ge 0 \Leftrightarrow \frac{{{x^2} + x}}{{x - 1}} \ge 0 \Leftrightarrow - 1 \le x \le 0 \vee x > 1\]
Đáp án cần chọn là: D
Câu 32:
Cho phương trình \[{11^x} + m = {\log _{11}}\left( {x - m} \right)\] với m là tham số. Có bao nhiêu giá trị nguyên của \[m \in \left( { - 205;205} \right)\;\] để phương trình đã cho có nghiệm?
 Xem đáp án
Xem đáp án
Bước 1: Sử dụng hàm đặc trưng.
Ta có
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\,{{11}^x} + m = {{\log }_{11}}\left( {x - m} \right)}\\{ \Leftrightarrow {{11}^x} + x = x - m + {{\log }_{11}}\left( {x - m} \right)}\\{ \Leftrightarrow {{11}^x} + x = {{11}^{{{\log }_{11}}\left( {x - m} \right)}} + {{\log }_{11}}\left( {x - m} \right)\,\,\left( * \right)}\end{array}\]
Xét hàm số\[f\left( t \right) = {11^t} + t \Rightarrow y' = {11^t}.\ln 11 + 1 > 0\,\,\,\forall t\] Khi đó hàm số\[y = f\left( t \right)\] đồng biến trên\(\mathbb{R}\)
Do đó\[\left( * \right) \Leftrightarrow x = {\log _{11}}\left( {x - m} \right) \Leftrightarrow {11^x} = x - m \Leftrightarrow m = x - {11^x}\]
Bước 2: Khảo sát hàm số \[g(x) = x - {11^x}\]
Xét hàm số\[g\left( x \right) = x - {11^x}\] ta có
\[g'\left( x \right) = 1 - {11^x}.\ln 11 = 0 \Rightarrow x = {\log _{11}}\frac{1}{{\ln 11}} = {x_0}\]
Bảng biến thiên:
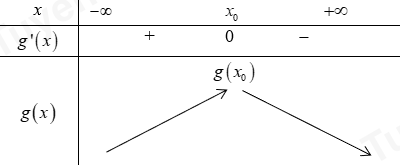
Bước 3: Biện luận nghiệm theo m.
Để phương trình đã cho có nghiệm thì\[m < g\left( {{x_0}} \right) \approx - 0,78\]
Kết hợp điều kiện đề bài ta có\(\left\{ {\begin{array}{*{20}{c}}{ - 205 < m \le - 1}\\{m \in \mathbb{Z}}\end{array}} \right.\)
Vậy có 204 giá trị của nguyên của m thỏa mãn yêu cầu bài toán.
Câu 33:
Xét các số thực dương a và b thỏa mãn \[{\log _3}\left( {1 + ab} \right) = \frac{1}{2} + {\log _3}\left( {b - a} \right)\]. Giá trị nhỏ nhất của biểu thức \[P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}}\] bằng:
 Xem đáp án
Xem đáp án
Bước 1: Tìm điều kiện và tìm mối quan hệ giữa a và b từ đẳng thức bài cho.
ĐKXĐ:\(\left\{ {\begin{array}{*{20}{c}}{b - a > 0}\\{a,b > 0}\end{array}} \right.\)
Ta có:
\[\begin{array}{*{20}{l}}{{{\log }_3}\left( {1 + ab} \right) = \frac{1}{2} + {{\log }_3}\left( {b - a} \right)}\\{ \Leftrightarrow {{\log }_3}\left( {1 + ab} \right) - {{\log }_3}\left( {b - a} \right) = \frac{1}{2}}\\{ \Leftrightarrow {{\log }_3}\frac{{1 + ab}}{{b - a}} = \frac{1}{2}}\\{ \Leftrightarrow \frac{{1 + ab}}{{b - a}} = \sqrt 3 }\\{ \Leftrightarrow 1 + ab = \sqrt 3 \left( {b - a} \right)}\\{ \Leftrightarrow \frac{1}{a} + b = \sqrt 3 \left( {\frac{b}{a} - 1} \right)}\end{array}\]
Bước 2: Sử dụng BĐT Cô-si để đánh giá\[\frac{a}{b}\]
Áp dụng BĐT Cô-si ta có\[\frac{1}{a} + b \ge 2\sqrt {\frac{b}{a}} \] nên\[\sqrt 3 \left( {\frac{b}{a} - 1} \right) \ge 2\sqrt {\frac{b}{a}} \Leftrightarrow \sqrt 3 \frac{b}{a} - 2\sqrt {\frac{b}{a}} - \sqrt 3 \ge 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt {\frac{b}{a}} \ge \sqrt 3 }\\{\sqrt {\frac{b}{a}} \le - \frac{1}{{\sqrt 3 }}(Loai)}\end{array}} \right. \Leftrightarrow \sqrt {\frac{b}{a}} \ge \sqrt 3 \Leftrightarrow \frac{b}{a} \ge 3\)
Bước 3: Sử dụng BĐT Cô-si để đánh giá P.
Ta có: \[P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}} = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}}\]
Áp dụng BĐT Cô-si ta có \[1 + {a^2}{b^2} \ge 2\sqrt {{a^2}{b^2}} = 2ab\] nên
\[1 + {a^2} + {b^2} + {a^2}{b^2} \ge {a^2} + {b^2} + 2ab = {\left( {a + b} \right)^2}\]
\[ \Rightarrow P = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}} \ge \frac{{{{\left( {a + b} \right)}^2}}}{{a\left( {a + b} \right)}} = \frac{{a + b}}{a} = 1 + \frac{b}{a} \ge 4\]
Vậy
\[{P_{min}} = 4 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} = b}\\{\frac{b}{a} = 3}\\{a,b > 0,b - a > 0}\end{array}} \right.\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} = 3a}\\{b = 3a}\\{a,b > 0,b - a > 0}\\{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{\sqrt 3 }}}\\{b = \sqrt 3 }\end{array}} \right.\)
Câu 34:
Xét các số thực x,y thỏa mãn \[{2^{{x^2} + {y^2} + 1}} \le ({x^2} + {y^2} - 2x + 2){4^x}\]. Giá trị lớn nhất của biểu thức \[P = \frac{{8x + 4}}{{2x - y + 1}}\;\] là \[a + \sqrt a \].Tìm a
 Xem đáp án
Xem đáp án
Bước 1: Chia cả 2 vế của bất phương trình cho\[{4^x}\] và đặt \[t = {x^2} + {y^2} - 2x + 1\]
Nhận xét:\[{x^2} + {y^2} - 2x + 2 = {\left( {x - 1} \right)^2} + {y^2} + 1 > 0\,\,\,\forall x,y\]
Bpt \[ \Leftrightarrow {2^{{x^2} + {y^2} - 2x + 1}} \le {x^2} + {y^2} - 2x + 2\]
Đặt\[t = {x^2} + {y^2} - 2x + 1\] bất phương trình trở thành\[{2^t} \le t + 1 \Leftrightarrow {2^t} - t - 1 \le 0\]
Bước 2: Xét hàm đặc trưng\[f\left( t \right) = {2^t} - t - 1\] và đánh giá t từ đó đánh giá\[{\left( {x - 1} \right)^2} + {y^2}\]
Xét hàm số\[f\left( t \right) = {2^t} - t - 1\] có\[f'\left( t \right) = {2^t}\ln 2 - 1 = 0 \Leftrightarrow t = {\log _2}\left( {{{\log }_2}e} \right).\]
BBT:
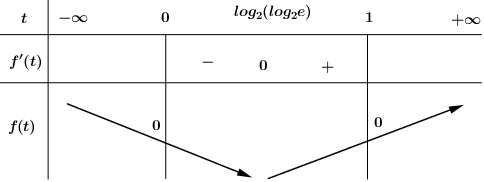
Suy ra ta có\[0 \le t \le 1 \Rightarrow {\left( {x - 1} \right)^2} + {y^2} \le 1\]
Bước 3: Biến đổi P và tìm min, max
Ta có:
\[P = \frac{{8x + 4}}{{2x - y + 1}} \Leftrightarrow 2Px - Py + P = 8x + 4\]
\[ \Leftrightarrow P - 4 = \left( {8 - 2P} \right)x + Py \Leftrightarrow 3P - 12 = \left( {8 - 2P} \right)\left( {x - 1} \right) + Py\]
\[ \Leftrightarrow {\left( {3P - 12} \right)^2} \le \left[ {{{\left( {8 - 2P} \right)}^2} + {P^2}} \right]\left[ {{{\left( {x - 1} \right)}^2} + {y^2}} \right]\]
\[ \Rightarrow {\left( {3P - 12} \right)^2} \le {\left( {8 - 2P} \right)^2} + {P^2} \Leftrightarrow 4{P^2} - 40P + 80 \le 0\]
\[ \Leftrightarrow 5 - \sqrt 5 \le P \le 5 + \sqrt 5 \]
Bước 4: Xét dấu “=” xảy ra
Dấu “=” xảy ra
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{8 - 2P}}{P} = \frac{{x - 1}}{y} = - \frac{2}{{\sqrt 5 }}}\\{{{(x - 1)}^2} + {y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 1 = - \frac{2}{{\sqrt 5 }}y}\\{\frac{9}{5}{y^2} = 1}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 \mp \frac{2}{3}}\\{y = \pm \frac{{\sqrt 5 }}{3}}\end{array}} \right.\end{array}\)
\[ \Rightarrow \max P = 5 + \sqrt 5 \] đạt được khi\[x = \frac{1}{3};y = \frac{{\sqrt 5 }}{3}\]
Vậy a=5
Câu 35:
Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty Bảo Việt với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12 triệu đồng với lãi suất hàng năm không đổi là 6% / năm. Hỏi sau đúng 18 năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân.
 Xem đáp án
Xem đáp án
Gọi số tiền đóng hàng năm là A=12 (triệu đồng), lãi suất là\[r = 6{\rm{\% }} = 0,06\]
Sau 1 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là\[{A_1} = A\left( {1 + r} \right)\] (nhưng người đó không rút mà lại đóng thêm A triệu đồng nữa, nên số tiền gốc để tính lãi năm sau là\[{A_1} + A\])
Sau 2 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_2} = \left( {{A_1} + A} \right)\left( {1 + r} \right) = \left[ {A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right) = A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Sau 3 năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\[\begin{array}{l}{A_3} = \left( {{A_2} + A} \right)\left( {1 + r} \right) = \left[ {A{{\left( {1 + r} \right)}^2} + A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right)\\ = A{\left( {1 + r} \right)^3} + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\end{array}\]
Sau 18 năm, người đó đi rút tiền thì sẽ nhận được số tiền là:
\[{A_{18}} = A{\left( {1 + r} \right)^{18}} + A{\left( {1 + r} \right)^{17}} + ... + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\]
Tính:\[{A_{18}} = A\left[ {{{\left( {1 + r} \right)}^{18}} + {{\left( {1 + r} \right)}^{17}} + ... + {{\left( {1 + r} \right)}^2} + \left( {1 + r} \right) + 1 - 1} \right]\]
\[ \Rightarrow {A_{18}} = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{{\left( {1 + r} \right) - 1}} - 1} \right] = A\left[ {\frac{{{{\left( {1 + r} \right)}^{19}} - 1}}{r} - 1} \right] = 12\left[ {\frac{{{{\left( {1 + 0,06} \right)}^{19}} - 1}}{{0,06}} - 1} \right] \approx 393,12\]
Đáp án cần chọn là: D
