Lớp 6A, 6B, 6C, 6D lần lượt có 35, 36, 39, 40 học sinh.
a) Lớp nào có thể chia thành 5 tổ có cùng số tổ viên?
b) Lớp nào có thể chia tất cả các bạn thành các đôi bạn học tập?
Giải bởi Vietjack
a) Để biết lớp nào có thể chia thành 5 tổ có cùng số tổ viên thì ta xét xem số học sinh của lớp đó có chia hết cho 5 hay không.
Ta có: 35 ⋮ 5 (vì 35 có chữ số tận cùng là 5)
40 ⋮ 5 (vì 40 có chữ số tận cùng là 0)
Nên: Lớp 6A và 6D có thể chia thành 5 tổ mà các tổ có cùng số tổ viên
b) Một đôi bạn thì gồm 2 bạn nên muốn biết lớp nào có thể chia tất cả các bạn thành các đôi bạn học tập thì ta xét xem số học sinh của mỗi lớp đó có chia hết cho 2 hay không.
Ta có: 36 ⋮ 2 (Vì 36 có chữ số tận cùng là 6)
40 ⋮ 2 (Vì 40 có chữ số tận cùng là 0)
Nên: Lớp 6B và 6D có thể chia tất cả các bạn thành các đôi bạn học tập.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chọn các số chia hết cho 5 ở dưới đây:
10; 22; 15; 27; 33; 25; 19; 36; 95.
Có nhận xét gì về các chữ số tận cùng (chữ số hàng đơn vị) của các số chia hết cho 5 em vừa chọn.
Tìm chữ số thích hợp thay cho dấu * để số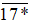 
thỏa mãn từng điều kiện:
a) Chia hết cho 2;
b) Chia hết cho 5;
c) Chia hết cho cả 2 và 5.
a) Viết hai số lớn hơn 1000 và chia hết cho 2.
b) Viết hai số lớn hơn 100 và không chia hết cho 2.
Bà Huệ có 19 quả xoài và 40 quả quýt. Bà có thể chia số quả này thành 5 phần bằng nhau (có cùng số xoài, có cùng số quýt mà không được cắt quả) được không?
Không thực hiện phép tính, em hãy cho biết những tổng (hiệu) nào sau đây chia hết cho 2, chia hết cho 5.
a) 146 + 550;
b) 575 – 40;
c) 3.4.5 + 83;
d) 7.5.6 - 35.4
Trong một đại hội thể thao có các đội và số người tham gia trong các bảng sau:
Trong các đội đã cho, đội nào xếp được thành hai hàng có số người bằng nhau?
Trong những số sau: 2 023; 19 445; 1 010, số nào:
a) chia hết cho 2?
b) chia hết cho 5?
c) chia hết cho 10?
