Giải bởi Vietjack
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức của bài toán R thay đổi để \[{U_{RL}}\] không đổi khi đó: \[\left\{ {\begin{array}{*{20}{l}}{{U_{RL}} = U}\\{{Z_C} = 2{Z_L}}\end{array}} \right.\]
Cách giải:
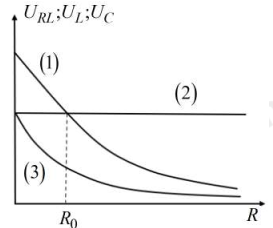
Từ đồ thị, ta nhận xét: đường (2) là \[{U_{RL}} = h{\rm{/}}s\]
R thay đổi để \[{U_{RL}}\]không đổi khi đó: \[\left\{ {\begin{array}{*{20}{l}}{{U_{RL}} = U}\\{{Z_C} = 2{Z_L}}\end{array}} \right.\]
Khi đó, đường (1) là \[{U_C},\]đường (2) là \[{U_L}\]
+ Tại giá trị \[R = {R_0}\] thì: \[{U_C} = {U_{RL}} = U \Leftrightarrow \frac{U}{{\sqrt {R_0^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} \cdot {Z_C} = U\]
+ Tại \[R = 3{R_0} = 3\sqrt 3 {Z_L}\]
Khi đó, độ lệch pha giữa u và i:
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
