30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 23)
-
5998 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Khoảng cách giữa 2 lần dây duỗi thẳng: \[\frac{T}{2}\]
+ Sử dụng biểu thức sóng dừng trên dây 1 đầu cố định, 1 đầu tự do: \[l = (2k + 1)\frac{\lambda }{4}\]
Trong đó số nút sóng = số bụng sóng = k + 1.
+ Sử dụng biểu thức tính vận tốc truyền sóng trên dây: \[v = \frac{\lambda }{T}\]
Cách giải:
+ Khoảng thời gian giữa 6 lần liên tiếp sợi dây duỗi thẳng là: \[\frac{{5T}}{2} = 0,25 \Rightarrow T = 0\]
+ Điều kiện có sóng dừng: \[l = (2k + 1)\frac{\lambda }{4}\]
Có 8 nút song
Tốc độ truyền sóng trên dây: \[v = \frac{\lambda }{T} = \frac{{0,24}}{{0,1}} = 2,4m{\rm{/}}s\]
Chọn B.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về dòng điện trong các môi trường.
Cách giải:
Hạt tải điện trong chất điện phân là ion dương và ion âm.
Chọn C.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về hiện tượng tán sắc ánh sáng.
Cách giải:
Chùm sáng hẹp khi đi qua lăng kính mà không bị tán sắc thì chứng tỏ ánh sáng được sử dụng là ánh sáng đơn sắc.
Chọn D.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận tốc truyền âm trong các môi trường: \[{v_r} > {v_l} > {v_k}\]
Cách giải:
Ta có vận tốc truyền âm trong các môi trường: \[{v_r} > {v_l} > {v_k}\]
⇒ Tốc độ truyền âm trong khí ôxi là nhỏ nhất trong các môi trường trên.
Chọn A.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về các loại dao động
Cách giải:
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Chọn C.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng điều kiện xảy ra hiện tượng quang điện: hay ε ≥ A
Cách giải:
Ta có, hiện tượng quang điện xảy ra đối với kim loại đó nếu hay ε ≥ A
Chọn B.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính chu kì dao động của con lắc lò xo: \[T = 2\pi \sqrt {\frac{m}{k}} \]
Cách giải:
Ta có:
Chọn D.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về hiện tượng quang điện trong.
Cách giải:
Hiện tượng được giải thích dựa vào hiện tượng quang điện trong là hiện tượng điện trở suất của một chất quang dẫn giảm mạnh khi được chiếu sáng.
Chọn B.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Tiên đề về sự bức xạ và hấp thụ năng lượng:
Cách giải:
Nguyên tử cần hấp thụ một photon có năng lượng bằng:
Chọn D.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính khoảng vân: \[i = \frac{{\lambda D}}{a}\]
+ Sử dụng biểu thức xác định vị trí vân sáng: \[{x_S} = ki\]
Cách giải:
Vị trí vân sáng bậc 3: \[{x_{{S_3}}} = 3i = 3\frac{{\lambda D}}{a} = 3\frac{{\lambda {{.10}^3}a}}{a} = {3.10^3}\lambda \]
Chọn D.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về các loại quang phổ.
Cách giải:
A – sai vì quang phổ liên tục do các chất rắn, lỏng, khí ở nhiệt độ cao phát ra và là dải màu biến thiên liên tục từ đỏ đến tím.
B, C, D - đúng
Chọn A.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về các loại tia.
Cách giải:
Khi ta nung nóng một kim loại ở nhiệt độ cao các bức xạ có thể phát ra là: tia hồng ngoại, ánh sáng nhìn thấy và tia tử ngoại. Bức xạ không thể có là tia X.
Do nguồn gốc của tia X: Chùm electron có năng luợng lớn đập vào kim loại nguyên tử lượng lớn → làm phát ra tia X
Chọn A.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính cảm ứng từ tại tâm của dòng điện tròn: \[B = 2\pi {.10^{ - 7}}\frac{I}{r}\]
Cách giải:
Cảm ứng từ tại tâm của dòng điện tròn: \[B = 2\pi {.10^{ - 7}}\frac{I}{r}\]
Thay số ta được: \[B = 2\pi {.10^{ - 7}}\frac{{10}}{{0,2}} = \pi {.10^{ - 5}}T\]
Chọn D.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính dung kháng: \[{Z_C} = \frac{1}{{\omega C}}\]
Cách giải:
Dung kháng của tụ điện: \[{Z_C} = \frac{1}{{\omega C}}\]
Chọn C.Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính bước sóng:
Cách giải:
Bước sóng có giá trị bằng:
Chọn D.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức \[{I_0} = \sqrt {\frac{C}{L}} {U_0}\]
+ Sử dụng biểu thức tính giá trị hiệu dụng: \[I = \frac{{{I_0}}}{{\sqrt 2 }}\]
Cách giải:
Ta có:
Chọn D.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Biên độ dao động tổng hợp: \[A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } \]
Cách giải:
Biên độ dao động tổng hợp: \[A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } \]
Hai dao động cùng pha có
Chọn B.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Độ lệch pha của u so với i:
Cách giải:
Theo bài ra ta có:
Độ lệch pha giữa u và i:
⇒ u nhanh pha hơn i một góc \[\frac{\pi }{3}\] hay i trễ pha hơn u một góc 3\[\frac{\pi }{3}\]
Chọn C.Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính tần số góc:
+ Sử dụng biểu thức tính vận tốc cực đại: \[{v_{\max }} = \omega {S_0} = \omega .l{\alpha _0}\]
Cách giải:
Tốc độ của con lắc khi qua vị trí cân bằng
Chọn B.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng điều kiện giao thoa sóng cơ học.
Cách giải:
Để hai sóng có thể giao thoa được với nhau thì chúng phải xuất phát từ hai nguồn kết hợp là hai nguồn có cùng phương, cùng tần số và có độ lệch pha không thay đổi theo thời gian.
Chọn D.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức xác định tần số dao động của con lắc đơn: \[f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \]
Cách giải:
Tần số dao động của con lắc đơn là: \[f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \]
Chọn A.Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Tần số của máy phát điện xoay chiều một pha: \[f = np\]
Trong đó: p là số cặp cực; n (vòng/s) là tốc độ quay của roto
Cách giải:
Ta có: n vòng/giờ \[ = \frac{n}{{3600}}\] vòng/s
⇒ Từ thông qua mỗi cuộn dây của stato biến thiên tuần hoàn với tần số: \[f = \frac{{np}}{{3600}}(Hz)\]
Chọn C.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về thu phát sóng điện từ
Cách giải:
Bộ phận trong máy phát thanh vô tuyến dùng để biến đổi trực tiếp dao động âm thành dao động điện có cùng tần số là micro.
Chọn D.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức liên hệ giữa gia tốc và li độ:
Cách giải:
Gia tốc của vật có giá trị cực đại: \[{a_{\max }} = {\omega ^2}A\]
Chọn A.Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Vận dụng biểu thức tính công suất hao phí: \[\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R\]
+ Sử dụng biểu thức của máy biến áp lí tưởng: \[\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\]
Cách giải:
Công suất hao phí: \[\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R \Rightarrow \Delta P \sim \frac{1}{{{U^2}}}\]
Để công suất hao phí giảm 2500 lần thì hiệu điện thế tăng lần
\[ \Rightarrow \frac{{{U_2}}}{{{U_1}}} = 50 \Rightarrow \frac{{{N_2}}}{{{N_1}}} = 50\]
Chọn B.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính tần số của mạch dao động: \[f = \frac{1}{{2\pi \sqrt {LC} }}\]
Cách giải:
Từ công thức tính tần số: \[f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C = \frac{1}{{4{\pi ^2}{f^2}.L}}\]
\[ \Rightarrow C = \frac{1}{{4{\pi ^2}.{{\left( {{{100.10}^6}} \right)}^2}{{.0,5.10}^{ - 6}}}} = {5,066.10^{ - 12}}F = 5,066pF\]
Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức liên hệ giữa hiệu điện thế và cường độ điện trường: \[E = \frac{U}{d}\]
Cách giải:
Ta có: \[E = \frac{U}{d}\]
Trong đó U có đơn vị Vôn (V); d có đơn vị là mét (m) ⇒ V/m là đơn vị của cường độ điện trường.
Chọn A.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về nguồn điện.
Cách giải:
Trong một mạch điện kín, lực làm di chuyển các điện tích bên trong nguồn điện, giữa hai cực của nguồn là lực lạ.
Chọn A.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về sóng dừng:
+ Khoảng cách giữa hai bụng sóng hoặc hai nút sóng liên tiếp là \[\frac{\lambda }{2}\]
+ Khoảng cách giữa một bụng sóng và một nút sóng liên tiếp là \[\frac{\lambda }{4}\]
+ Hai điểm đối xứng nhau qua nút luôn dao động ngược pha.
Cách giải:
A, B, D - đúng
C – sai vì: Hai điểm đối xứng nhau qua nút luôn dao động ngược pha.
Chọn C.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc phương trình u, i.
+ Sử dụng biểu thức tính công suất: \[P = UI\cos \varphi \]
+ Sử dụng biểu thức tính giá trị cực đại: \[{U_0} = U\sqrt 2 \]
Cách giải:
+ Độ lệch pha giữa u và i:
+ Công suất tiêu thụ của đoạn mạch:
Chọn A.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính năng lượng của photon:
+ Sử dụng biểu thức tính công suất phát xạ: \[P = \frac{{n\varepsilon }}{t}\]
Cách giải:
Số photon mà nguồn đó phát ra trong 1 giây: \[n = \frac{{Pt}}{\varepsilon } = \frac{{Pt}}{{\frac{{hc}}{\lambda }}} = \frac{{1.1}}{{\frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{600.10}^{ - 9}}}}}} = {3,02.10^{18}}\] hạt
Chọn C.Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính quãng đường lớn nhất vật đi được trong thời gian \[\Delta t:{S_{\max }} = 2A\sin \frac{{\Delta \varphi }}{2}\]
+ Sử dụng biểu thức tính quãng đường nhỏ nhất vật đi được trong thời gian \[\Delta t:{S_{\min }} = 2A\left( {1 - \cos \frac{{\Delta \varphi }}{2}} \right)\]
Cách giải:
+ Quãng đường lớn nhất vật đi được trong thời gian \[\Delta t:{S_{\max }} = 2A\sin \frac{{\Delta \varphi }}{2}\]
+ Quãng đường nhỏ nhất vật đi được trong thời gian \[\Delta t:{S_{\min }} = 2A\left( {1 - \cos \frac{{\Delta \varphi }}{2}} \right)\]
Với \[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{S_{\max }} = 2.10\sin \frac{\pi }{4} = 10\sqrt 2 cm}\\{{S_{\min }} = 2.10\left( {1 - \cos \frac{\pi }{4}} \right) = 20 - 10\sqrt 2 cm}\end{array}} \right.\]
Quãng đường vật có thể đi được: \[{S_{\min }} \le S \le {S_{\max }} \Leftrightarrow 5,858m \le S \le 14,14m\]
⇒ Trong khoảng thời gian 0,5s quãng đường vật có thể đi được là: 8cm.
Chọn B.Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Vận dụng biểu thức tính cảm kháng và dung kháng: \[\left\{ {\begin{array}{*{20}{l}}{{Z_L} = \omega L}\\{{Z_C} = \frac{1}{{\omega C}}}\end{array}} \right.\]
+ Sử dụng biểu thức tính hệ số công suất:
Cách giải:
+ Khi \[f = {f_2} = 50Hz:\cos {\varphi _2} = 1 \Rightarrow {Z_{{L_2}}} = {Z_{{C_2}}} \Leftrightarrow \frac{1}{{LC}} = \omega _2^2\]
+ Khi \[f = {f_1} = 25Hz:\left\{ {\begin{array}{*{20}{l}}{{Z_{{L_1}}} = \frac{{{\omega _1}}}{{{\omega _2}}}{Z_{{L_2}}} = \frac{{{Z_{{L_2}}}}}{2}}\\{{Z_{{C_1}}} = \frac{{{\omega _2}}}{{{\omega _1}}}{Z_{{C_2}}} = 2{Z_{{C_2}}} = 2{Z_{{L_2}}}}\end{array}} \right.\]
\[ \Rightarrow \cos {\varphi _1} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)}^2}} }} = \frac{R}{{\sqrt {{R^2} + \left( {\frac{{{Z_{{L_2}}}}}{2} - 2{Z_{{L_2}}}} \right)} }} = \frac{{\sqrt 2 }}{2}\] \[ \Rightarrow 2{R^2} = {R^2} + \frac{9}{4}Z_{{L_2}}^2 \Rightarrow {Z_{{L_2}}} = \frac{2}{3}R\]
+ Khi \[f = {f_3} = 75Hz:\left\{ {\begin{array}{*{20}{l}}{{Z_{{L_3}}} = \frac{{{\omega _3}}}{{{\omega _2}}}{Z_{{L_2}}} = \frac{{3{Z_{{L_2}}}}}{2}}\\{{Z_{{C_3}}} = \frac{{{\omega _2}}}{{{\omega _3}}}{Z_{{C_2}}} = \frac{2}{3}{Z_{{C_2}}} = \frac{2}{3}{Z_{{L_2}}}}\end{array}} \right.\]
\[ \Rightarrow \cos {\varphi _3} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_3}}} - {Z_{{C_3}}}} \right)}^2}} }} = \frac{R}{{\sqrt {{R^2} + \left( {\frac{{3{Z_{{L_2}}}}}{2} - \frac{2}{3}{Z_{{L_2}}}} \right)} }} = 0,874\] Chọn B.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp:
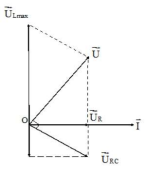
Vận dụng bài toán L thay đổi để \[{U_{{L_{\max }}}}\] khi đó \[\left\{ {\begin{array}{*{20}{l}}{{U_{RC}} \bot {U_{AB}}}\\{U_{L\max }^2 = {U^2} + U_{RC}^2 = {U^2} + U_R^2 + U_C^2}\\{{U_{L\max }}.{U_R} = U.{U_{RC}}}\\{\frac{1}{{U_R^2}} = \frac{1}{{{U^2}}} + \frac{1}{{U_{RC}^2}}}\end{array}} \right.\]
Cách giải:
Ta có: L thay đổi để \[{U_{{L_{\max }}}}\] khi đó: \[U_{L\max }^2 = {U^2} + U_{RC}^2\]
Lại có: \[\frac{1}{{U_R^2}} = \frac{1}{{{U^2}}} + \frac{1}{{U_{RC}^2}} \Rightarrow {U_R} = 25\sqrt 3 V\]
Độ lệch pha giữa điện áp giữa hai đầu mạch điện AB và điện áp giữa hai đầu điện trở:
Chọn C.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính bước sóng:
+ Sử dụng biểu thức tính số cực đại trên đường thẳng nối 2 nguồn cùng pha: \[ - \frac{L}{\lambda } < k < \frac{L}{\lambda }\]
Cách giải:
+ Bước sóng:
+ Số điểm dao động với biên độ cực đại trên MN bằng số giá trị k nguyên thỏa mãn:
Có 21 giá trị của k nguyên thỏa mãn. Vậy có 21 điểm
Chọn B.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
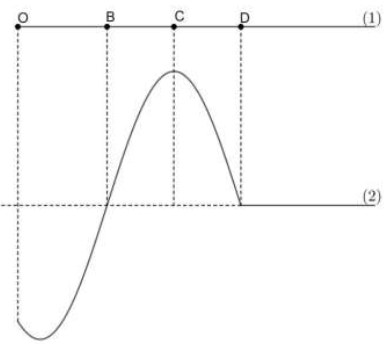
+ Đọc đồ thị động năng theo thời gian
+ Sử dụng vòng tròn lượng giác.
+ Sử dụng biểu thức tính khoảng cách: \[d = \sqrt {\Delta {d^2} + \Delta {u^2}} \]
+ Sử dụng biểu thức tính tốc độ truyền sóng: v = λ.f
+ Sử dụng biểu thức tính vận tốc dao động cực đại:
Cách giải:
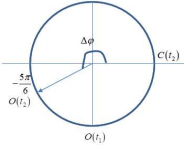
Từ hình ảnh và dữ kiện đề bài ta có vòng tròn lượng giác:
Có:
Độ lệch pha giữa 2 điểm O và C:
Tại thời điểm t1 khoảng cách giữa O và C: \[{d_1} = OC\] (ở trạng thái cân bằng)
Tại thời điểm t2 khoảng cách giữa O và C:
Theo đề bài, ta có:
\[ \Rightarrow \frac{v}{{{v_{\max }}}} = \frac{{\lambda f}}{{\omega a}} = \frac{{\lambda f}}{{2\pi f.a}} = \frac{\lambda }{{2\pi a}} = \frac{5}{{2\pi }} \approx 0,8\]
Chọn C.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Công suất hao phí: \[\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R\]
+ Công suất có ích: \[{P_{ci}} = P - \Delta P\]
Cách giải:
Gọi P là công suất nơi phát, n là số bóng đèn nhà vườn sử dụng.
Tổng công suất các bóng đèn tiêu thụ: \[P' = 220n = P - \Delta P\]
\[ \Rightarrow 220n = P - \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R = P - \frac{{{P^2}}}{{{{1500}^2}}}.50\]
\[ \Rightarrow 50{P^2} - {22,5.10^5}P + {49,5.10^7}.n = 0\]
Để phương trình có nghiệm thì:
\[ \Leftrightarrow {\left( {{{22,5.10}^5}} \right)^2} - {4.50.49,5.10^7}n \ge 0 \Leftrightarrow n \le 51,136 \Rightarrow {n_{\max }} = 51\]
⇒ Số bóng tối đa mà nhà vườn có thể sử dụng cùng lúc là 51 bóng.
Chọn A.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức xác định vị trí vân sáng, vân tối: \[\left\{ {\begin{array}{*{20}{l}}{{x_S} = ki}\\{{x_t} = \left( {k + \frac{1}{2}} \right)i}\end{array}} \right.\]
+ Sử dụng biểu thức tính khoảng vân: \[i = \frac{{\lambda D}}{a}\]
Cách giải:
Xét 11 vân tối liên tiếp tính từ vân trung tâm.
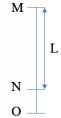
+ Ta có: \[L = 15 = 10{i_ \equiv } \Rightarrow {i_ \equiv } = 1,5mm\]
+ Khoảng vân: \[{i_1} = \frac{{{\lambda _1}D}}{a} = 0,5mm\]
\[ + \left\{ {\begin{array}{*{20}{l}}{{x_N} = 0,5{i_ \equiv } = 1,5{i_1}}\\{{x_M} = 10,5{i_ \equiv } = 31,5{i_1}}\end{array}} \right.\]
Ta thấy \[{N_1} = 30,{N_{12}} = 10 \Rightarrow {N_1} + {N_2} - {N_{12}} = 70 \Rightarrow {N_2} = 50 \Rightarrow {\lambda _2} < {\lambda _1}\]
Tại N: \[{x_N} = 1,5{i_1} = 2,5{i_2} \Rightarrow 1,5{\lambda _1} = 2,5{\lambda _2} \Rightarrow {\lambda _2} = 0,45\mu m\]
Chọn D.
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị
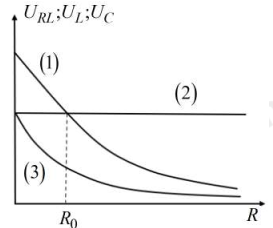
+ Sử dụng biểu thức của bài toán R thay đổi để \[{U_{RL}}\] không đổi khi đó: \[\left\{ {\begin{array}{*{20}{l}}{{U_{RL}} = U}\\{{Z_C} = 2{Z_L}}\end{array}} \right.\]
Cách giải:
Từ đồ thị, ta nhận xét: đường (2) là \[{U_{RL}} = h{\rm{/}}s\]
R thay đổi để \[{U_{RL}}\]không đổi khi đó: \[\left\{ {\begin{array}{*{20}{l}}{{U_{RL}} = U}\\{{Z_C} = 2{Z_L}}\end{array}} \right.\]
Khi đó, đường (1) là \[{U_C},\]đường (2) là \[{U_L}\]
+ Tại giá trị \[R = {R_0}\] thì: \[{U_C} = {U_{RL}} = U \Leftrightarrow \frac{U}{{\sqrt {R_0^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} \cdot {Z_C} = U\]
+ Tại \[R = 3{R_0} = 3\sqrt 3 {Z_L}\]
Khi đó, độ lệch pha giữa u và i:
Chọn D.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
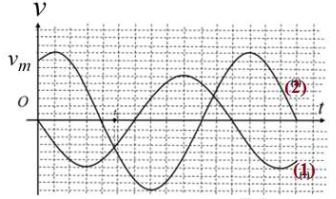
+ Đọc đồ thị
+ Chuẩn hóa số liệu
+ Vận dụng vòng tròn lượng giác
+ Sử dụng hệ thức trong tam giác: \[{a^2} = {b^2} + {c^2} - 2bc.\cos (a)\]
Cách giải:
Đặt 1 ô có giá trị bằng 1
Từ đồ thị ta có:
+ Chu kì: T = 12 ô
Độ lệch pha giữa 2 dao động:
Chuẩn hóa:
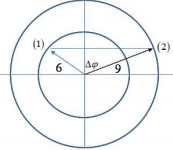
Khoảng cách giữa hai vật tại thời điểm t1:
Chọn A.
