Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Vệ tinh địa tĩnh bay trên quỹ đạo Trái Đất có cùng chu kì với chu kì tự quay của Trái Đất
Gia tốc trọng trường tại độ cao h: \(g = \frac{{GM}}{{{{(R + h)}^2}}}\)
Tần số góc:
Thời gian sóng điện từ truyền trong không gian: \(t = \frac{s}{c}\)
Cách giải:
Ta có hình vẽ:
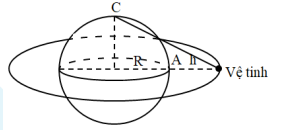
Vệ tinh ở độ cao h so với mặt đất
Gia tốc chuyển động của vệ tinh là: \(g = \frac{{GM}}{{{{(R + h)}^2}}}\)
Tần số góc chuyển động của vệ tinh là:
Vệ tinh chuyển động với chu kig bằng chu kì tự quay quanh trục của Trái Đất, ta có:
\(T = \frac{{2\pi \sqrt {{{(R + h)}^3}} }}{{\sqrt {GM} }} = 86400 \Rightarrow h \approx {35897.10^3}(\;{\rm{m}})\)
Thời gian sóng truyền từ trạm phát A đến vệ tinh là: \({t_1} = \frac{h}{c}\)
Trạm thu C đặt trên cùng một đường kinh tuyến với A và cách A xa nhất
→ C nằm tại 1 trong 2 cực của Trái Đất
Khoảng cách từ vệ tinh tới trạm thu C là: \(l = \sqrt {{{(R + h)}^2} + {R^2}} \)
Thời gian sóng truyền từ vệ tinh tới trạm thu C là: \({t_2} = \frac{l}{c} = \frac{{\sqrt {{{(R + h)}^2} + {R^2}} }}{c}\)
Thời gian tín hiệu truyền từ trạm A đến vệ tinh rồi đến trạm thu C là:
\(\Delta t = {t_1} + 0,5 + {t_2} = \frac{h}{c} + 0,5 + \frac{{\sqrt {{{(R + h)}^2} + {R^2}} }}{c} = 0,5 + \frac{{h + \sqrt {{{(R + h)}^2} + {R^2}} }}{c}\)
\( \Rightarrow \Delta t = 0,5 + \frac{{{{35897.10}^3} + \sqrt {{{\left( {{{64.10}^5} + {{35897.10}^3}} \right)}^2} + {{\left( {{{64.10}^5}} \right)}^2}} }}{{{{3.10}^8}}} \approx 0,762(s)\)
→ Giá trị ∆t gần nhất với giá trị 0,759 s
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết