30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 25)
-
5916 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Năng lượng photon:
Cách giải:
Năng lượng của photon ứng với bức xạ này là:
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết sơ đồ khối của máy phát thanh
Cách giải:
Các bộ phận có trong sơ đồ khối của máy phát thanh đơn giản là: micrô, anten phát, mạch biến điệu.
Chọn A.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết dao động cưỡng bức
Cách giải:
Biên độ của dao động cưỡng bức phụ thuộc vào biên độ của ngoại lực tuần hoàn tác dụng lên vật, tần số của ngoại lực tác dụng lên vật, lực cản môi trường tác dụng lên vật
→ Biên độ của dao động cưỡng bức không phụ thuộc vào bản chất của ngoại lực cưỡng bức
Chọn D.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Hiệu đường đi của ánh sáng từ hai khe đến vị trí vân tối: \({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
Cách giải:
Hiệu đường đi của ánh sáng từ hai khe đến vị trí vân tối là: \({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
Tại điểm M có: \({k_{\min }} = 0 \Rightarrow {\left( {{d_2} - {d_1}} \right)_{\min }} = \frac{\lambda }{2}\)
Chọn B.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Từ trường của dòng điện chạy trong dây dẫn thẳng dài: \(B = {2.10^{ - 7}}\frac{I}{r}\)
Cách giải:
Từ trường của dòng điện chạy trong dây dẫn thẳng dài là: \(B = {2.10^{ - 7}}\frac{I}{r} \Rightarrow B\~I\)
Cường độ dòng điện trong dây dẫn tăng thêm 15 A, ta có:
\({I_2} = {I_1} + 15 = 20(A) \Rightarrow {I_2} = 4{I_1} \Rightarrow {B_2} = 4{B_1} = 4.0,5 = 2(\mu T)\)
Chọn A.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết dòng điện không đổi
Cách giải:
Dòng điện không đổi là dòng điện có chiều và cường độ không thay đổi theo thời gian.
Chọn D.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết hai nguồn sóng kết hợp
Cách giải:
Hai nguồn sóng kết hợp là hai nguồn dao động cùng phương, cùng tần số và có hiệu số pha không đổi theo thời gian
Chọn D.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết máy biến áp
Cách giải:
Máy biến áp là thiết bị dùng để thay đổi điện áp xoay chiều mà không làm thay đổi tần số
Chọn A.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Tốc độ của vật dao động điều hòa: \(v = \omega \sqrt {{A^2} - {x^2}} \)
Gia tốc của dao động điều hòa:
Lực kéo về tác dụng lên vật dao động điều hòa: \({F_{kv}} = ma = - m{\omega ^2}x\)
Cách giải:
Lực kéo về tác dụng lên vật dao động điều hòa là: \({F_{kv}} = - m{\omega ^2}x\)
Độ lớn cực đại của gia tốc là:
Vận tốc có độ lớn cực đại là: \(|v{|_{\max }} = \omega A \Leftrightarrow x = 0 \to {\rm{D}}\) đúng
Chọn D.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết sóng dọc
Cách giải:
Sóng dọc truyền được trong các môi trường rắn, lỏng, khí
Chọn B.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Vị trí vân sáng: \({x_s} = ki\)
Cách giải:
Khoảng cách từ vân sáng bậc 3 tới vân sáng trung tâm là:
\({x_s} = ki \Rightarrow {2,4.10^{ - 3}} = 3.i \Rightarrow i = {8.10^{ - 4}}(\;{\rm{m}})\)
Lại có khoảng vân:
Chọn A.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết đường sức điện
Cách giải:
Qua mỗi điểm trong điện trường ta chỉ có thể vẽ được một đường sức điện → A sai
Các đường sức điện không bao giờ cắt nhau → B đúng
Nơi nào điện trường mạnh hơn thì nơi đó đường sức điện được vẽ mau hơn → C sai
Các đường sức điện xuất phát từ các điện tích dương và tận cùng ở các điện tích âm → D sai
Chọn B.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Các vecto \(\vec E,\vec B\) và hướng truyền sóng đôi một vuông góc với nhau tuân theo quy tắc bàn tay phải: đặt bàn tay phải sao cho vecto \(\overrightarrow B \) hướng vào lòng bàn tay, ngón tay cái choãi ra chỉ chiều của \(\overrightarrow E \) , bốn ngón tay hướng theo chiều truyền sóng điện từ
Trong sóng điện từ, điện trường và từ trường luôn biến thiên cùng pha: \(\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}}\)
Cách giải:
Nhận xét: điện trường và từ trường biến thiên cùng pha, ta có:
\(\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}} = \frac{1}{2} \Rightarrow B = \frac{{{B_0}}}{2}\)
Áp dụng quy tắc bàn tay phải, ta có hình vẽ:
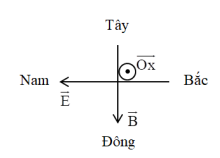
Từ hình vẽ ta thấy vecto cảm ứng từ hướng về phía Đông
Chọn C.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
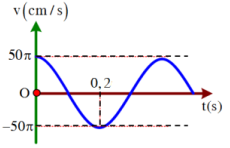
Sử dụng kĩ năng đọc đồ thị
Vận tốc biến thiên sớm pha \(\frac{\pi }{2}{\rm{rad}}\) so với li độ
Li độ biến thiên cùng chu kì với vận tốc
Cách giải:
Từ đồ thị ta thấy khoảng thời gian ngắn nhất vận tốc biến thiên từ giá trị cực đại đến cực tiểu là:
\(\frac{T}{2} = 0,2(s) \Rightarrow T = 0,4(s)\)
Từ đồ thị ta thấy ở thời điểm đầu, vận tốc có giá trị cực đại → pha ban đầu của dao động là:
Chọn A.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Hạt nhân
Cách giải:
Hạt nhân \(_8^{17}O\) có 8 proton và 9 notron
Chọn B.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Cường độ hiệu dụng của dòng điện xoay chiều bằng cường độ của một dòng điện không đổi, nếu cho hai dòng điện đó lần lượt đi qua cùng một điện trở trong những khoảng thời gian bằng nhau đủ dài thì nhiệt lượng tỏa ra bằng nhau
Cách giải:
Số chỉ của Ampe kế nhiệt cho biết cường độ dòng điện hiệu dụng trong mạch
Chọn D.Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết dòng điện trong chất điện phân
Cách giải:
Dòng điện trong chất điện phân là ion dương và ion âm
Chọn C.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết hiện tượng quang – phát quang
Cách giải:
Hiện tượng quang - phát quang là sự hấp thụ ánh sáng có bước sóng này để phát ra ánh sáng có bước sóng khác
Chọn C.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
Tần số của con lắc lò xo: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \)
Cách giải:
Tần số của con lắc lò xo là: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \)
Chọn C.Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng thang sóng điện từ:
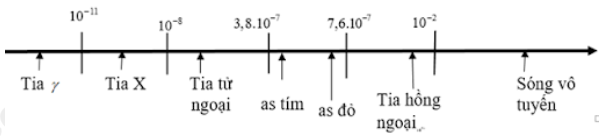
Cách giải:
Trong các tia: tia hồng ngoại, tia tử ngoại, tia X và tia đơn sắc lục, tia có tần số nhỏ nhất là tia hồng ngoại
Chọn A.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững
Cách giải:
Năng lượng liên kết riêng của các hạt nhân là:
Chọn A.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Các định luật bảo toàn trong phản ứng hạt nhân: bảo toàn số nuclon, bảo toàn điện tích, bảo toàn năng lượng toàn phần, bảo toàn động lượng
Cách giải:
Các định luật bảo toàn trong phản ứng hạt nhân là: bảo toàn số nuclon, bảo toàn điện tích, bảo toàn năng lượng toàn phần, bảo toàn động lượng
→ Trong phản ứng hạt nhân không có định luật bảo toàn khối lượng nghỉ
Chọn B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết thuyết lượng tử ánh sáng
Cách giải:
Thuyết lượng tử ánh sáng không được dùng để giải thích hiện giao thoa ánh sáng
Chọn D.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết hiện tượng khúc xạ ánh sáng
Cách giải:
Chiết suất của chất làm lăng kính thay đổi theo tần số ánh sáng qua lăng kính
Chọn C.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
Hệ số công suất của mạch điện xoay chiều:
Cách giải:
Hệ số công suất của mạch điện là:
\(\cos \left( {{\varphi _u} - {\varphi _i}} \right) = \cos \left( {\frac{\pi }{3} - \frac{\pi }{6}} \right) = \cos \frac{\pi }{6} \approx 0,87\)
Chọn C.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức cường độ dòng điện: \(i = {I_0}\cos (\omega t + \varphi )\)
Với i là cường độ dòng điện tức thời
I0 là cường độ dòng điện cực đại
ω là tần số góc
\(\varphi \) là pha ban đầu
\((\omega t + \varphi )\) là pha tại thời điểm t
Cách giải:
Cường độ dòng điện \(i = 2\cos 100\pi t(A)\) có pha tại thời điểm t là 100πt rad
Chọn B.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Trên sóng dừng, những điểm đối xứng với nhau qua nút sóng luôn dao động ngược pha
Những điểm đối xứng với nhau qua bụng sóng luôn dao động cùng pha
Cách giải:
Điểm C là một nút sóng, hai điểm trên dây đối xứng với nhau qua C dao động ngược pha
Chọn A.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Mức cường độ âm: \(L = \lg \frac{I}{{{I_0}}}(B) = 10\lg \frac{I}{{{I_0}}}(dB)\)
Cách giải:
Mức cường độ âm được xác định là: \(L = \lg \frac{I}{{{I_0}}}(B) = 10\lg \frac{I}{{{I_0}}}(dB)\)
Chọn B.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Khoảng vân:
Giá trị trung bình:
Sai số tỉ đối: \(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}\)
Sai số tuyệt đối trung bình:
Cách giải:
Khoảng cách giữa 11 vân sáng là 10 khoảng vân, ta có:
Sai số tuyệt đối của khoảng vân là:
\(10\Delta i = \frac{{\Delta {i_1} + \Delta {i_2} + \Delta {i_3} + \Delta {i_4} + \Delta {i_5}}}{5} \Rightarrow \Delta i = \frac{{1 + 0,5 + 1 + 0,5 + 0}}{{50}} = 0,06(\;{\rm{mm}})\)
Giá trị trung bình của bước sóng là:
Ta có sai số tỉ đối:
\(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}} \Rightarrow \frac{{\Delta \lambda }}{{0,65}} = \frac{0}{{{{0,5.10}^{ - 3}}}} + \frac{{0,06}}{{1,3}} + \frac{{0,1}}{{100}}\)
Chọn A.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
Định luật bảo toàn năng lượng điện từ: \({{\rm{W}}_d} = {{\rm{W}}_t} \Rightarrow \frac{1}{2}CU_0^2 = \frac{1}{2}LI_0^2\)
Công thức độc lập với thời gian: \(\frac{{{q^2}}}{{q_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
Chu kì dao động riêng của mạch: \(T = 2\pi \sqrt {LC} \)
Cách giải:
Áp dụng định luật bảo toàn năng lượng điện từ trong mạch, ta có:
\({{\rm{W}}_{d{\rm{max}}}} = {{\rm{W}}_{t\max }} \Rightarrow \frac{1}{2}{\rm{CU}}_0^2 = \frac{1}{2}LI_0^2 \Rightarrow I_0^2 = \frac{{CU_0^2}}{L} = \frac{{C{{.12}^2}}}{{{{9.10}^{ - 3}}}} = 16000{\rm{C}}\)
Áp dụng công thức độc lập với thời gian, ta có:
Chu kì dao động riêng của mạch là:
Chọn A.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện tại một điểm là cực đại giao thoa: \(MA - MB = k\lambda \)
Điều kiện tại một điểm là cực tiểu giao thoa: \(NA - NB = (k + 0,5)\lambda \)
Số điểm dao động với biên độ cực đại trên đoạn thẳn AB thỏa mãn:
Cách giải: Ta có hình vẽ:
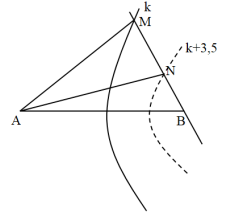
Giả sử tại M là cực đại bậc k
Giữa M, N có 3 cực đại nữa → tại N là cực tiểu thức k + 3,5
Ta có:
Đặt hai nguồn sóng tại MN, điểm B nằm trên đường thẳng MN, số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:
→ Trên AB có 4 điểm dao động với biên độ cực đại
Chọn D.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
Vệ tinh địa tĩnh bay trên quỹ đạo Trái Đất có cùng chu kì với chu kì tự quay của Trái Đất
Gia tốc trọng trường tại độ cao h: \(g = \frac{{GM}}{{{{(R + h)}^2}}}\)
Tần số góc:
Thời gian sóng điện từ truyền trong không gian: \(t = \frac{s}{c}\)
Cách giải:
Ta có hình vẽ:
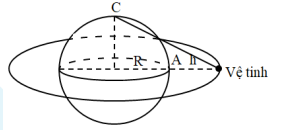
Vệ tinh ở độ cao h so với mặt đất
Gia tốc chuyển động của vệ tinh là: \(g = \frac{{GM}}{{{{(R + h)}^2}}}\)
Tần số góc chuyển động của vệ tinh là:
Vệ tinh chuyển động với chu kig bằng chu kì tự quay quanh trục của Trái Đất, ta có:
\(T = \frac{{2\pi \sqrt {{{(R + h)}^3}} }}{{\sqrt {GM} }} = 86400 \Rightarrow h \approx {35897.10^3}(\;{\rm{m}})\)
Thời gian sóng truyền từ trạm phát A đến vệ tinh là: \({t_1} = \frac{h}{c}\)
Trạm thu C đặt trên cùng một đường kinh tuyến với A và cách A xa nhất
→ C nằm tại 1 trong 2 cực của Trái Đất
Khoảng cách từ vệ tinh tới trạm thu C là: \(l = \sqrt {{{(R + h)}^2} + {R^2}} \)
Thời gian sóng truyền từ vệ tinh tới trạm thu C là: \({t_2} = \frac{l}{c} = \frac{{\sqrt {{{(R + h)}^2} + {R^2}} }}{c}\)
Thời gian tín hiệu truyền từ trạm A đến vệ tinh rồi đến trạm thu C là:
\(\Delta t = {t_1} + 0,5 + {t_2} = \frac{h}{c} + 0,5 + \frac{{\sqrt {{{(R + h)}^2} + {R^2}} }}{c} = 0,5 + \frac{{h + \sqrt {{{(R + h)}^2} + {R^2}} }}{c}\)
\( \Rightarrow \Delta t = 0,5 + \frac{{{{35897.10}^3} + \sqrt {{{\left( {{{64.10}^5} + {{35897.10}^3}} \right)}^2} + {{\left( {{{64.10}^5}} \right)}^2}} }}{{{{3.10}^8}}} \approx 0,762(s)\)
→ Giá trị ∆t gần nhất với giá trị 0,759 s
Chọn B.
Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
Định luật bảo toàn động lượng:
Công thức hàm cos: \({a^2} = {b^2} + {c^2} + 2bc\cos \varphi \)
Năng lượng tỏa ra của phản ứng: \(\Delta E = {K_s} - {K_t}\)
Mối liên hệ giữa động lượng và động năng: \({p_X}^2 = 2{m_X}{K_X}\)
Cách giải:
Năng lượng tỏa ra của phản ứng là:
\(\Delta E = {K_C} + {K_n} - {K_a} \Rightarrow 5,6 = {K_C} + {K_n} - 5\)
\( \Rightarrow {K_C} + {K_n} = 10,6({\rm{MeV}}) \Rightarrow {K_n} = 10,6 - {K_C}\)
Áp dụng định luật bảo toàn động lượng, ta có:
\({p_\alpha }^2 = {p_C}^2 + {p_n}^2 + 2{p_C}{p_n}\cos {80^0}\)
Chọn B.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện có sóng dừng trên dây với hai đầu dây cố định: \(l = k\frac{\lambda }{2}\) với k là số bó sóng
Hai điểm thuộc cùng một bó sóng hoặc thuộc hai bó sóng cùng chẵn hoặc cùng lẻ thì dao động cùng pha Hai điểm thuộc hai bó sóng liền kề, hoặc 1 điểm thuộc bó sóng chẵn, 1 điểm thuộc bó sóng lẻ dao động ngược pha
Cách giải:
Ta có chiều dài sợi dây AB là:
trên dây có 5 bó sóng
Tại vị trí cân bằng của điểm M có:
điểm M thuộc bó sóng thứ 4 (bó sóng chẵn)
Nhận xét: trên mỗi bó sóng có 2 điểm dao động cùng biên độ với điểm M
→ trên mỗi bó sóng lẻ (k = 1; 3; 5) có 2 điểm dao động cùng biên độ, ngược pha với M
→ Trên dây có 6 điểm dao động cùng biên độ, ngược pha với điểm M
Chọn B.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
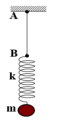
Độ biến dạng của lò xo khi ở vị trí cân bằng: \(\Delta l = \frac{{mg}}{k}\)
Tần số góc của con lắc lò xo:
Tốc độ của vật ở vịt rí cân bằng: \({v_{\max }} = \omega A\)
Công thức độc lập với thời gian: \({v^2} = \omega \sqrt {{A^2} - {x^2}} \)
Thời gian chuyển động ném thẳng đứng lên: \(t = \frac{v}{g}\)
Độ cao vật đạt được trong chuyển động ném thẳng đứng hướng lên: \({h_{\max }} = \frac{{{v^2}}}{{2g}}\)
Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)
Tốc độ trung bình: \({v_\phi } = \frac{S}{t}\)
Cách giải:
Tần số góc của con lắc là:
Độ biến dạng của lò xo khi ở vị trí cân bằng là:
\(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{50}} = 0,05(\;{\rm{m}}) = 5(\;{\rm{cm}})\)
Nhận xét: con lắc dao động khi lực đàn hồi có độ lớn bằng 0, dây bị chùng, hệ chuyển động với gia tốc trọng trường g
→ Từ thời điểm vật đạt li độ -5 cm đến khi nó đạt độ cao cực đại lần thứ nhất, vật chuyển động giống như chuyển động ném thẳng đứng lên với vận tốc v
Ta có vòng tròn lượng giác:
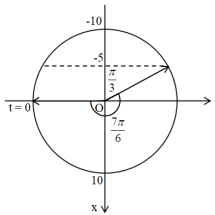
Vật dao động điều hòa trong khoảng thời gian từ thời điểm đầu đến thời điểm đầu tiên lò xo không biến dạng (x = -5 cm), vecto quay được góc là:
Quãng đường vật dao động điều hòa là:
\({s_1} = 2A + (A - \Delta l) = 3A - \Delta l = 3.10 - 5 = 25(\;{\rm{cm}})\)
Ở li độ x = -5 cm, áp dụng công thức độc lập với thời gian, ta có vận tốc của vật là:
Vật chuyển động ném lên, quãng đường vật chuyển động được đến khi dừng lại là:
\({s_2} = {h_{\max }} = \frac{{{v^2}}}{{2g}} = \frac{{{{(0,5\sqrt 6 )}^2}}}{{2.10}} = 0,075(\;{\rm{m}}) = 7,5(\;{\rm{cm}})\)
Thời gian vật chuyển động ném lên là: \({t_2} = \frac{v}{g} = \frac{{0,5\sqrt 6 }}{{10}} = \frac{{\sqrt 6 }}{{20}}(s)\)
Tốc độ trung bình của vật là:
\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{25 + 7,5}}{{\frac{{7\pi }}{{60\sqrt 2 }} + \frac{{\sqrt 6 }}{{20}}}} \approx 85,16(\;{\rm{cm}}/{\rm{s}})\)
Chọn D.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
Lực điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = m{\omega ^2}r\)
Tần số của chuyển động tròn đều: \(f = \frac{\omega }{{2\pi }}\)
Cách giải:
Lực điện tác dụng lên electron là:
Tần số chuyển động của electron quanh hạt nhân là:
Chọn C.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
Điện áp hiệu dụng giữa hai đầu đoạn mạch chứa điện trở và cuộn dây thuần cảm: \({U_{LR}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Điện áp hiệu dụng giữa hai đầu tụ điện: \({U_C} = \frac{{U \cdot {Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_L} = \frac{{U \cdot {Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Sử dụng kĩ năng đọc đồ thị
Sử dụng phương pháp chuẩn hóa số liệu cos
Hệ số công suất của mạch điện:
Cách giải:
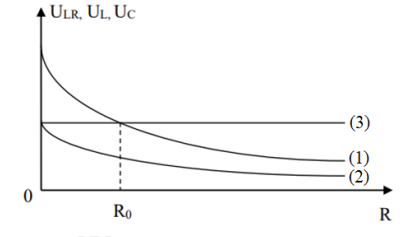
Ta có đồ thị:
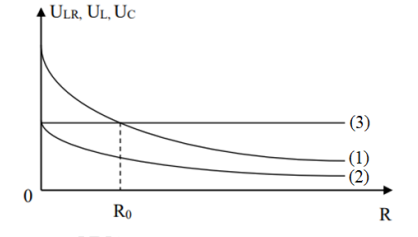
Điện áp hiệu dụng giữa hai đầu đoạn mạch gồm cuộn cảm thuần L và biến trở R, điện áp hiệu dụng hai đầu tụ C, điện áp hiệu dụng hai đầu cuộn cảm thuần L là:
\(\left\{ {\begin{array}{*{20}{l}}{{U_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{{\sqrt {1 + \frac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}}\\{{U_C} = \frac{{U.{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}}\\{{U_L} = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}}\end{array}} \right.\)
Nhận xét: khi R tăng có UC và UL giảm → đồ thị (3) là đồ thị URL
Từ đồ thị ta thấy đồ thị (3) không phụ thuộc vào R
Để URL không phụ thuộc vào R, ta có:
\({Z_C}^2 - 2{Z_L}{Z_C} = 0 \Rightarrow {Z_C} = 2{Z_L} \Rightarrow {U_C} = 2{U_L}\)
Ta thấy với mọi giá trị của R luôn có \({U_C} = 2{U_L} \to \) đồ thị (1) là UC, đồ thị (2) là UL
Lại có: \({U_{RL}} = \frac{U}{{\sqrt {1 + \frac{0}{{{R^2} + Z_L^2}}} }} = U\)
Chuẩn hóa \({Z_L} = 1 \Rightarrow {Z_C} = 2\)
Tại giá trị \(R = {R_0} \Rightarrow {U_C} = {U_{RL}} = U\)
Khi
Chọn D.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
Biên độ của con lắc lò xo nằm ngang: \(A = {l_{\max }} - {l_0}\)
Động năng bằng n lần thế năng: W1
Cách giải:
Biên độ dao động của con lắc là: \(A = {l_{\max }} - {l_0} = 38 - 30 = 8(\;{\rm{cm}})\)
Tại vị trí động năng bằng n lần thế năng và vị trí thế năng bằng n lần động năng, ta có:
Trường hợp 1: hai vị trí này ở cùng một phía so với vị trí cân bằng, khoảng cách giữa hai vị trí là:
Trường hợp 2: hai vị trí này ở hai phía so với vị trí cân bằng khoảng cách giữa hai vị trí là:
Nhận xét: khoảng cách ngắn nhất giữa hai vị trí này là:
Vậy giá trị lớn nhất của n gần nhất với 5
Chọn C.
Câu 39:
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng phương pháp giản đồ vecto
Định lí hàm sin: \(\frac{a}{{\sin \hat A}} = \frac{b}{{\sin \hat B}} = \frac{c}{{\sin \hat C}}\)
Gia tốc cực đại của dao động điều hòa: \({a_{\max }} = {\omega ^2}A\)
Cách giải:
Ta có giản đồ vecto:
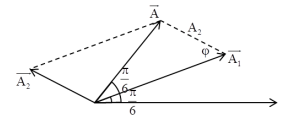
Từ giản đồ vecto, áp dụng định lí hàm sin, ta có:
\(\frac{{{A_2}}}{{\sin \frac{\pi }{6}}} = \frac{A}{{\sin \varphi }} \Rightarrow \frac{A}{{\sin \varphi }} = \frac{4}{{\sin \frac{\pi }{6}}} = 8 \Rightarrow A = 8\sin \varphi \)
Để độ lớn gia tốc của vật đạt giá trị lớn nhất:
\({a_{\max }} \Leftrightarrow {A_{\max }} \Rightarrow {(\sin \varphi )_{\max }} = 1 \Rightarrow {A_{\max }} = 8(\;{\rm{cm}})\)
\( \Rightarrow {a_{\max }} = {\omega ^2}{A_{\max }} = {10^2}.8 = 800\left( {\;{\rm{cm}}/{{\rm{s}}^2}} \right) = 8\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Chọn C.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
Dung kháng của tụ điện: \({Z_c} = \frac{1}{{\omega C}}\)
Cường độ dòng điện hiệu dụng: \(I = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch và cường độ dòng điện:
Công suất tiêu thụ của đoạn mạch: \(P = UI\cos \varphi \)
Cách giải:
Dung kháng của tụ điện là:
Cường độ dòng điện trong mạch là:
\(I = \frac{{{U_{MM}}}}{{\sqrt {R_1^2 + Z_C^2} }} = \frac{{50}}{{\sqrt {{{40}^2} + {{40}^2}} }} = \frac{5}{{4\sqrt 2 }}(A)\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch AM và cường độ dòng điện là:
Công suất tiêu thụ của đoạn mạch MB là:
\({P_{MB}} = {U_{MB}}.I.\cos {\varphi _{MB}} = \frac{{150}}{{\sqrt 2 }} \cdot \frac{5}{{4\sqrt 2 }} \cdot \cos \frac{\pi }{3} = 46,875(\;{\rm{W}}) \approx 46,9(\;{\rm{W}})\)
Chọn D.
