 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
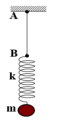
Độ biến dạng của lò xo khi ở vị trí cân bằng: \(\Delta l = \frac{{mg}}{k}\)
Tần số góc của con lắc lò xo:
Tốc độ của vật ở vịt rí cân bằng: \({v_{\max }} = \omega A\)
Công thức độc lập với thời gian: \({v^2} = \omega \sqrt {{A^2} - {x^2}} \)
Thời gian chuyển động ném thẳng đứng lên: \(t = \frac{v}{g}\)
Độ cao vật đạt được trong chuyển động ném thẳng đứng hướng lên: \({h_{\max }} = \frac{{{v^2}}}{{2g}}\)
Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)
Tốc độ trung bình: \({v_\phi } = \frac{S}{t}\)
Cách giải:
Tần số góc của con lắc là:
Độ biến dạng của lò xo khi ở vị trí cân bằng là:
\(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{50}} = 0,05(\;{\rm{m}}) = 5(\;{\rm{cm}})\)
Nhận xét: con lắc dao động khi lực đàn hồi có độ lớn bằng 0, dây bị chùng, hệ chuyển động với gia tốc trọng trường g
→ Từ thời điểm vật đạt li độ -5 cm đến khi nó đạt độ cao cực đại lần thứ nhất, vật chuyển động giống như chuyển động ném thẳng đứng lên với vận tốc v
Ta có vòng tròn lượng giác:
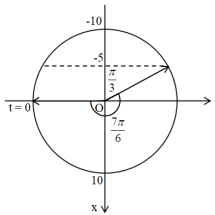
Vật dao động điều hòa trong khoảng thời gian từ thời điểm đầu đến thời điểm đầu tiên lò xo không biến dạng (x = -5 cm), vecto quay được góc là:
Quãng đường vật dao động điều hòa là:
\({s_1} = 2A + (A - \Delta l) = 3A - \Delta l = 3.10 - 5 = 25(\;{\rm{cm}})\)
Ở li độ x = -5 cm, áp dụng công thức độc lập với thời gian, ta có vận tốc của vật là:
Vật chuyển động ném lên, quãng đường vật chuyển động được đến khi dừng lại là:
\({s_2} = {h_{\max }} = \frac{{{v^2}}}{{2g}} = \frac{{{{(0,5\sqrt 6 )}^2}}}{{2.10}} = 0,075(\;{\rm{m}}) = 7,5(\;{\rm{cm}})\)
Thời gian vật chuyển động ném lên là: \({t_2} = \frac{v}{g} = \frac{{0,5\sqrt 6 }}{{10}} = \frac{{\sqrt 6 }}{{20}}(s)\)
Tốc độ trung bình của vật là:
\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{25 + 7,5}}{{\frac{{7\pi }}{{60\sqrt 2 }} + \frac{{\sqrt 6 }}{{20}}}} \approx 85,16(\;{\rm{cm}}/{\rm{s}})\)
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết