 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
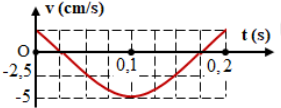
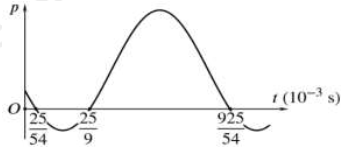
+ Đọc đồ thị
+ Sử dụng biểu thức tính độ dãn của lò xo tại \({\rm{VTCB}}:\Delta l = \frac{{mg}}{k}\)
+ Sử dụng biểu thức tính thế năng đàn hồi: \({{\rm{W}}_{dh}} = \frac{1}{2}k\Delta {l^2}\) với\({\rm{ }}\Delta l\)là độ biến dạng của lò xo
+ Sử dụng biểu thức tính thế năng trọng trường:
Cách giải:
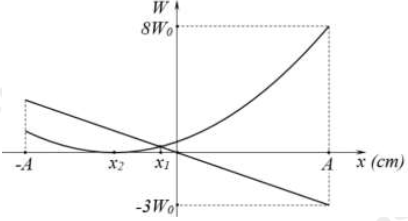
Từ đồ thị, ta thấy thế năng đàn hồi cực tiểu = 0 tại x2 \( \Rightarrow \) đây chính là độ dãn của lò xo tại VTCB
Lại có:
+ Thế năng đàn hồi: \({{\rm{W}}_{{\rm{d}}h}} = \frac{1}{2}k{\left( {x - {x_2}} \right)^2}\)
+ Thế năng trọng trường:
Từ đồ thị:
+ Xét tại
Theo đề bài ta có: \({x_1} - {x_2} = 3,66\;{\rm{cm}} \Rightarrow \) thay vào (*) ta suy ra:
+ Xét tại
Thay số vào ta suy ra:\(\frac{8}{{ - 3}} = \frac{{{{(A + 4,9997)}^2}}}{{2 \cdot A( - 4,9997)}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{A = 14,9991\;{\rm{cm}}}\\{A = 1,667\;{\rm{cm}}}\end{array}} \right.\)
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết