30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 27)
-
6110 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Lí thuyết về quang phổ vạch phát xạ:
+ Quang phổ vạch là một hệ thống các vạch sáng riêng lẻ, ngăn cách nhau bởi những khoảng tối.
+ Quang phổ vạch do các chất khí hay hơi ở áp suất thấp phát ra khi bị kích thích bằng điện hay bằng nhiệt.
+ Quang phổ vạch của các nguyên tố khác nhau thì rất khác nhau về số lượng các vạch, về vị trí và độ sáng tỉ đối giữa các vạch. Mỗi nguyên tố hóa học có một quang phổ vạch đặc trưng của nguyên tố đó.
+ Ứng dụng: Để phân tích cấu tạo chất.
Cách giải:
Quang phổ vạch phát xạ do chất khí ở áp suất thấp bị nung nóng phát ra.
Chọn A.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về đặc trưng sinh lí và đặc trưng vật lí của âm.
+ Đặc trưng sinh lí: Độ cao, độ to, âm sắc.
+ Đặc trưng vật lí: Tần số, cường độ âm, mức cường độ âm, đồ thị âm.
Cách giải:
Đặc trưng vật lí của âm là tần số.
Chọn C.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Máy biến áp là thiết bị hoạt động dựa trên hiện tượng cảm ứng điện từ, dùng để biến đổi điện áp xoay chiều mà không làm thay đổi tần số của nó.
+ Máy biến áp gồm hai cuộn dây có số vòng khác nhau quấn trên một lõi sắt kín. Lõi thường làm bằng các lá sắt hoặc thép pha silic, ghép cách điện với nhau để giảm hao phí điện năng do dòng Fu-cô.
+ Cuộn sơ cấp nối với nguồn điện xoay chiều, cuộn thứ cấp nối với tải tiêu thụ điện năng.
Cách giải:
A – đúng vì máy biến áp là thiết bị biến đổi điện áp xoay chiều và hoạt động dựa trên hiện tượng cảm ứng điện từ.
B, C, D – sai.
Chọn A.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về: Hấp thụ và phản xạ lọc lựa ánh sáng, màu sắc các vật.
Cách giải:
Khi chiếu chùm sáng trắng vào vật ta thấy nó có màu đỏ ⇒Vật này hấp thụ các ánh sáng khác và phản xạ lại ánh sáng đỏ.
⇒Nếu chiếu vào vật chùm ánh sáng màu lục thì vật sẽ hấp thụ hoàn toàn chùm ánh sáng đó và nó trở thành có màu đen, do đó ta sẽ không nhìn thấy vật.
Chọn B.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về các loại dao động
Cách giải:
Cộng hưởng cơ xảy ra ở dao động cưỡng bức.
Chọn C.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về dòng điện trong chất điện phân: Dòng điện trong lòng chất điện phân là dòng ion dương và ion âm chuyển động có hướng theo hai chiều ngược nhau.
Cách giải:
Hạt tải điện trong chất điện phân là ion dương và ion âm.
Chọn D.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng định nghĩa về đơn vị của các đại lượng vật lí.
+ Đơn vị của hiệu điện thế là V (Vôn).
+ Đơn vị của công suất là Oát (W).
+ Đơn vị của cường độ dòng điện là Ampe (A).
+ Đơn vị của cường độ điện trường là V/m (Vôn/mét)
Cách giải:
Công thức liên hệ giữa hiệu điện thế và cường độ điện trường: \(E = \frac{U}{d}\)
Cường độ điện trường E có đơn vị là: Vôn/ mét (V/m)
Chọn D.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về pha trong các mạch điện xoay chiều.
Biểu thức của cường độ dòng điện và các điện áp tức thời:
Cách giải:
Ta có các biểu thức:
Độ lệch pha: Trong mạch điện xoay chiều, \({u_L}\) và \({u_C}\) ngược pha nhau.
Chọn C.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng tiên đề về bức xạ, hấp thụ năng lượng:
+ Khi nguyên tử chuyển từ trạng thái dừng có năng lượng En sang trạng thái có năng lượng \({E_m} < {E_n}\) thì nó phát ra một photon có năng lượng ..
+ Ngược lại, nếu nguyên tử ở trạng thái dừng có năng lượng Em mà hấp thụ được một phôtôn có năng lượng hf đúng bằng hiệu \({E_n} - {E_m}\) thì nó chuyển sang trạng thái dừng có năng lượng En lớn hơn.
Cách giải:
Khi nguyên tử chuyển từ trạng thái dừng có năng lượng Ensang trạng thái dừng có năng lượng thấp hơn Em thì nó phát ra một photon có năng lượng:
Chọn D.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về các loại tia phóng xạ.
Cách giải:
Tia đâm xuyên mạnh nhất là tia γ.
Chọn B.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức xác định vị trí vân tối: \({x_t} = \left( {k + \frac{1}{2}} \right)i\)
Cách giải:
Vị trí vân tối: \({x_t} = \left( {k + \frac{1}{2}} \right)i\)
Vân tối thứ hai ứng với k =1 ⇒Khoảng cách từ vân sáng trung tâm đến vân tối thứ hai: \({x_{t2}} = \left( {1 + \frac{1}{2}} \right)i = \frac{3}{2}i\)
Chọn D.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức định luật Ôm: \(I = \frac{U}{Z}\)
Cách giải:
Biểu thức định luật Ôm:
Chọn B.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về tia X.
Cách giải:
A, B, D - đúng
C – sai vì tia X không mang điện tích nên không bị lệch trong điện trường và từ trường.
Chọn C.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
Đọc phương trình dao động: \(x = A\cos (\omega t + \varphi )\)
+ Biên độ dao động: A
+ Tần số góc: ω
+ Pha dao động tại thời điểm \({\rm{t}}:(\omega t + \varphi )\)
Cách giải:
Phương trình dao động: \(x = 2\sqrt 2 \cos (3t + 3\sqrt 3 )cm \Rightarrow \) Biên độ dao động: \(A = 2\sqrt 2 cm\)
Chọn D.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng ứng dụng của các loại sóng vô tuyến.
Cách giải:
Ta có bảng sau:
|
Loại sóng |
Bước sóng |
Đặc điểm |
Ứng dụng |
|
Sóng dài |
\( \ge 1000m\) |
+ Có năng lượng thấp + Bị các vật trên mặt đất hấp thụ mạnh nhưng nước lại hấp thụ ít |
Dùng trog thông tin liên lạc dưới nước |
|
Sóng trung |
\(100 - 1000m\) |
+ Ban ngày bị tầng điện li hấp thụ mạnh nên không truyền đi xa được + Ban đêm bị tầng điện li phản xạ nên truyền đi xa được |
Dùng trog thông tin liên lạc vào ban đêm |
|
Sóng ngắn |
\(10 - 100m\) |
+ Có năng lượng lớn + Bị phản xạ nhiều lần giữa tầng điện li và mặt đất |
Dùng trog thông tin liên lạc trên mặt đất |
|
Sóng cực ngắn |
\(1 - 10m\) |
+ Có năng lượng rất lớn + Không bị tâng điện li hấp thụ hay phản xạ + Xuyên qua tấng điện li vào vũ trụ |
Dùng trog thông tin vũ trụ |
Truyền hình vệ tinh sử dụng sóng cực ngắn.
Chọn D.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Khoảng cách giữa hai bụng sóng liên tiếp hay hai nút sóng liên tiếp trong sóng dừng là \(\frac{\lambda }{2}\) .
Khoảng cách giữa một bụng sóng và một nút sóng liên tiếp là \(\frac{\lambda }{4}\) .
Cách giải:
Khoảng cách giữa hai bụng sóng liên tiếp liên tiếp trong sóng dừng bằng nửa bước sóng.
Chọn A.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về tổng hợp dao động. \(\left\{ {\begin{array}{*{20}{l}}{{x_1} = {A_1} \cdot \cos \left( {2\pi f.t + {\varphi _1}} \right)}\\{{x_2} = {A_2} \cdot \cos \left( {2\pi f.t + {\varphi _2}} \right)}\\{x = {x_1} + {x_2} = A \cdot \cos (2\pi f.t + \varphi )}\end{array}} \right.\)
Cách giải:
Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số f là một dao động điều hòa có tần số bằng f .
Chọn B.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về cấu tạo hạt nhân nguyên tử.
Cách giải:
Khối lượng của proton và notron là: \({m_n} = 1,0078u;{m_p} = 1,0073u\)
A – sai vì: Notron có khối lượng lớn hơn khối lượng của proton.
B, C, D – đúng.
Chọn A.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính công suất của nguồn: P = EI
Cách giải:
Công suất của nguồn được tính bằng công thức: P = EI
Trong đó: E là suất điện động của nguồn điện, I là cường độ dòng điện chạy qua nguồn.
Chọn A.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính bước sóng:
Cách giải:
Sóng cơ truyền trong một môi trường vật chất với tần số f, tốc độ tuyền sóng v thì bước sóng là:
Chọn D.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Tần số góc, chu kì, tần số dao động của con lắc đơn:
Cách giải:
Tần số dao động của con lắc đơn: \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Chọn C.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
* Đọc phương trình dao động: \(x = A\cos (\omega t + \varphi )\)
+ Biên độ dao động: A
+ Tần số góc: ω
+ Pha dao động tại thời điểm \({\rm{t}}:(\omega t + \varphi )\)
* Công thức tính tần số: \(f = \frac{\omega }{{2\pi }}\)
Cách giải:
Phương trình dao động: \(x = 10\cos (4\pi t + \pi ){\rm{cm}} \Rightarrow \) Tần số góc:
⇒Tần số dao động của chất điểm: \(f = \frac{\omega }{{2\pi }} = \frac{{4\pi }}{{2\pi }} = 2\;{\rm{Hz}}\)
Chọn B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Trong quá trình truyền sóng, vecto cường độ điện trường \(\overrightarrow E \) và vecto cảm ứng từ \(\overrightarrow B \) biến thiên tuần hoàn theo không gian và thời gian, và luôn đồng pha.
Cách giải:
Do \(\overrightarrow E \) và \(\overrightarrow B \) biến thiên cùng pha với nhau nên: \(\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}}{\rm{ hay }}{\left( {\frac{E}{{{E_0}}}} \right)^2} = {\left( {\frac{B}{{{B_0}}}} \right)^2}\)
Chọn B.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính năng lượng của photon:
Cách giải:
Năng lượng của photon ứng với bức xạ có bước sóng 0,589μm:
Chọn A.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng các định luật bảo toàn để hoàn thiện phương trình:
+ Vận dụng định luật bảo toàn số \({\rm{Z}}:{Z_A} + {Z_B} = {Z_C} + {Z_D}\)
+ Vận dụng định luật bảo toàn số nuclon: \({A_A} + {A_B} = {A_C} + {A_D}\)
Cách giải:
Áp dụng định luật bảo toàn điện tích và bảo toàn số nuclon ta có:\(\left\{ {\begin{array}{*{20}{l}}{{A_X} + 19 = 4 + 16}\\{{Z_x} + 9 = 2 + 8}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{A_X} = 1}\\{{Z_X} = 1}\end{array}} \right.} \right.\)
⇒ X là proton.
Chọn D.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
Cảm ứng từ do dòng điện tròn gây ra tại tâm:
Cách giải:
Cảm ứng từ do 50 vòng dây điện tròn gây ra tại tâm của vòng dây:
Chọn B.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính hệ số công suất:
Cách giải:
Hệ số công suất của đoạn mạch gồm R nối tiếp với tụ điện:
Chọn A.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính giới hạn quang điện: \({\lambda _0} = \frac{{hc}}{A}\)
Cách giải:
Giới hạn quang điện của kim loại này là: \({\lambda _0} = \frac{{hc}}{A} = \frac{{6,625 \cdot {{10}^{ - 34}} \cdot 3 \cdot {{10}^8}}}{{6,625 \cdot {{10}^{ - 19}}}} = {3.10^{ - 7}}\;{\rm{m}} = 300\;{\rm{nm}}\)
Chọn C.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Công thức tính công suất hao phí: \(\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R\)
+ Hiệu suất truyền tải: \(H = \frac{{{P_{ci}}}}{P} = \frac{{P - \Delta P}}{P} = 1 - \frac{{\Delta P}}{P}\)
Cách giải:
+ Công suất hao phí: \(\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R = \frac{{{{\left( {{{10.10}^3}} \right)}^2}}}{{{{500}^2}{{.1}^2}}}2 = 800\;{\rm{W}}\)
+ Hiệu suất truyền tải điện: \(H = 1 - \frac{{\Delta P}}{P} = 1 - \frac{{800}}{{{{10.10}^3}}} = 0,92 = 92\% \)
Chọn A.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính bước sóng:
Cách giải:
Bước sóng của sóng này là:
Chọn D.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
Mức cường độ âm: \(L = 10 \cdot \log \frac{I}{{{I_0}}}(dB) = \log \frac{I}{{{I_0}}}(B)\)
Công thức logarit: \(\log a - \log b = \log \frac{a}{b}\)
Vận dụng biểu thức tính hiệu mức cường độ âm: \({L_2} - {L_1} = 10\log \frac{{{I_2}}}{{{I_1}}}(dB) = \log \frac{{{I_2}}}{{{I_1}}}(B)\)
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{L_M} = \log \frac{{{I_M}}}{{{I_0}}}(B)}\\{{L_N} = \log \frac{{{I_N}}}{{{I_0}}}(B)}\end{array} \Rightarrow {L_M} - {L_N} = \log \frac{{\frac{{{I_M}}}{{{I_0}}}}}{{\frac{{{I_N}}}{{{I_0}}}}} = \log \frac{{{I_M}}}{{{I_N}}}(B) \Rightarrow \frac{{{I_M}}}{{{I_N}}} = {{10}^{{L_M} - {L_N}}}} \right.\)
Chọn C.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
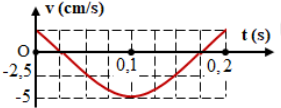
+ Đọc đồ thị v – t
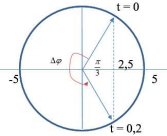
+ Sử dụng vòng tròn lượng giác.
+ Sử dụng công thức góc quét:
+ Sử dụng biểu thức tính vận tốc cực đại: \({v_{\max }} = A\omega \)
+ Sử dụng biểu thức: \({\varphi _v} - {\varphi _x} = \frac{\pi }{2}\)
Cách giải:
Từ đồ thị, ta có:
+ Vận tốc cực đại: \({v_{max}} = 5\;{\rm{cm}}/s\)
Vòng tròn lượng giác:
Từ vòng tròn lượng giác ta có:
Mặt khác:
Lại có:
Tại thời điểm ban đầu :
⇒ Phương trình li độ: \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)cm\)
Chọn C.
Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
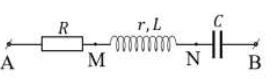
+ Sử dụng biểu thức tính hiệu điện thế của các đoạn mạch
+ Sử dụng biểu thức tính công suất:
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{U_R} = {U_{AM}} = 30V}\\{{U_{Lr}} = {U_{MN}} = 30V = \sqrt {U_r^2 + U_L^2} }\\{{U_C} = 100V}\\{U = 100V = \sqrt {{{\left( {{U_R} + {U_r}} \right)}^2} + {{\left( {{U_L} - {U_C}} \right)}^2}} }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{U_r^2 + U_L^2 = {{30}^2}}\\{{{\left( {30 + {U_r}} \right)}^2} + {{\left( {{U_L} - 100} \right)}^2} = {{100}^2}}\end{array}} \right.\)
+ Công suất tiêu thụ của đoạn mạch AB:
Chọn B.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Công thức tính bước sóng:
+ Công thức tính số điểm dao động với biên độ cực đại trong đoạn thẳng nối 2 nguồn cùng pha: \( - \frac{L}{\lambda } < k < \frac{L}{\lambda }\)
Cách giải:
+ Bước sóng:
+ Số điểm dao động với biên độ cực đại trên \({S_1}{S_2}\) bằng số giá trị k nguyên thỏa mãn:
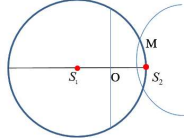
Gọi M là điểm dao động với biên độ cực đại trên vòng tròn cần tìm
M gần S2 ⇒M là cực đại bậc 6
Ta có:
Chọn C.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
+ Sử dụng biểu thức: \(\frac{{CU_0^2}}{2} = \frac{{LI_0^2}}{2}\)
Cách giải:
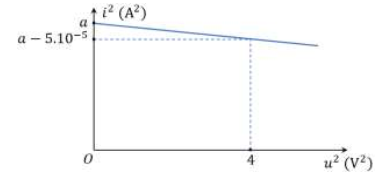
Trong mạch LC ta có: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
Từ đồ thị, ta có:
+ Tại \({u^2} = 0\) thì \({i^2} = a \Rightarrow I_0^2 = a\)
+ Tại \({u^2} = 4\) thì \({i^2} = a - {5.10^{ - 5}}\) ta suy ra: \(\frac{{a - 5 \cdot {{10}^{ - 5}}}}{{I_0^2}} + \frac{4}{{U_0^2}} = 1 \Leftrightarrow \frac{{a - 5 \cdot {{10}^{ - 5}}}}{a} + \frac{4}{{U_0^2}} = 1 \Rightarrow U_0^2 = 80000{\rm{a}}\)
Lại có:
\(I_0^2 = \frac{C}{L}U_0^2 \Leftrightarrow a = \frac{{{{2.10}^{ - 9}}}}{L} \cdot 80000a \Rightarrow L = {1,6.10^{ - 4}}H = 0,16mH\)
Chọn A.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Vận dụng pha dao động trong đoạn mạch xoay chiều
+ Sử dụng giản đồ véctơ quay.
+ Sử dụng hệ thức lượng trong tam giác.
Cách giải:
Do U hai đầu đoạn mạch không đổi và \({u_R} \bot {u_{LC}}\)
⇒Khi L thay đổi thì tập hợp các điểm M là đường tròn đường kính là hiệu điện thế giữa hai đầu đoạn mạch U =180 V
Mặt khác, độ lệch pha giữa u và I cũng là độ lệch pha giữa
Từ đó, ta có giản đồ véctơ điện áp như hình vẽ:
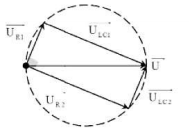
Từ giản đồ ta suy ra \({u_{{R_1}}} \bot {u_{{R_2}}} \Rightarrow U_{{R_1}}^2 + U_{{R_2}}^2 = U_{AB}^2 \Leftrightarrow {U^2} + 3{U^2} = {180^2} \Rightarrow U = 90\;{\rm{V}}\)
Chọn D.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức xác định vị trí trí vân tối: \({x_T} = \left( {k + \frac{1}{2}} \right)i\)
+ Số vân sáng trong khoảng L bất kì: \( - \frac{L}{i} < k < \frac{L}{i}\)
Cách giải:
+ Tại M và N là 2 vân tối ở hai phía so với vân sáng trung tâm ta suy ra:
\(\left\{ {\begin{array}{*{20}{l}}{{x_M} = M\;{{\rm{S}}_1} - M\;{{\rm{S}}_2} = \left( {{k_1} + \frac{1}{2}} \right)i \Rightarrow i = \frac{{{x_M}}}{{{k_1} + \frac{1}{2}}}}\\{{x_N} = N{S_1} - N{S_2} = \left( {{k_2} + \frac{1}{2}} \right)i}\end{array}} \right.\)
+ Số vân sáng trong khoảng MN thỏa mãn:
\(N{S_1} - N\;{{\rm{S}}_2} < ki < M{S_1} - M\;{{\rm{S}}_2} \Leftrightarrow \frac{{{x_N}}}{i} < k < \frac{{{x_M}}}{i} \Leftrightarrow {k_2} + \frac{1}{2} < k < {k_1} + \frac{1}{2}\)
Theo đề bài, giữa M và N có 9 vân sáng ⇒ có 9 giá trị của k
|
k1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
k2 |
- 9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
|
\({x_N}(\mu m)\) |
-29,75 |
-8,75 |
-4,55 |
-2,75 |
-1,75 |
-1,11 |
-0,67 |
|
Đáp án B |
Chọn B.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị p-t
+ Sử dung biểu thức tính công suất tức thời: p = ui
+ Sử dụng phương trình lượng giác.
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{u = {U_0}\cos \left( {\omega t + {\varphi _u}} \right)}\\{i = {I_0}\cos \left( {\omega t + {\varphi _i}} \right)}\end{array}} \right.\)
Đặt: \(\left\{ {\begin{array}{*{20}{l}}{{\varphi _u} + {\varphi _i} = x}\\{{\varphi _u} - {\varphi _i} = \varphi }\end{array}} \right.\)
Công suất tức thời: \(p = ui = UI.[\cos (2\omega t + x) + \cos \varphi ]\)
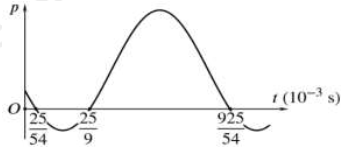
Từ đồ thị, ta thấy:
Công suất:
Tại
\( \Leftrightarrow \cos \left( {2\omega {t_1} + x} \right) = \cos \left( {2\omega {t_2} + x} \right) \Leftrightarrow \cos \left( {2.120\pi \frac{{{{25.10}^{ - 3}}}}{{54}} + x} \right) = \cos \left( {2.120\pi \frac{{25}}{9} \cdot {{10}^{ - 3}} + x} \right)\)
Thay vào (1) ta suy ra:
Chọn D.
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính bước sóng:
+ Sử dụng biểu thức tính số cực đại, cực tiểu giao thoa giữa 2 nguồn cùng pha.
+ Sử dụng biểu thức xác định cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)
Cách giải:
Ta có hình vẽ:
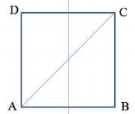
Lại có: C là nằm trên một cực đại giao thoa ⇒
Số cực tiểu trên AB thỏa mãn: \( - \frac{{AB}}{\lambda } - \frac{1}{2} < k < \frac{{AB}}{\lambda } - \frac{1}{2}\)
Trên AB có 28 cực tiểu (2) hay suy ra
⇒ Số cực đại trên AB là \(27 \Rightarrow n \le 13\) (3)
Từ (1) và (2) ta có
Từ (1), (3) và (4) ta có:
|
n |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
λ (cm) |
3,107 |
2,663 |
2,33 |
… |
… |
… |
… |
… |
|
v = λ.f (cm/s) |
34,17 |
29,29 |
25,63 |
… |
… |
… |
… |
… |
Chọn C.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức tính độ dãn của lò xo tại \({\rm{VTCB}}:\Delta l = \frac{{mg}}{k}\)
+ Sử dụng biểu thức tính thế năng đàn hồi: \({{\rm{W}}_{dh}} = \frac{1}{2}k\Delta {l^2}\) với\({\rm{ }}\Delta l\)là độ biến dạng của lò xo
+ Sử dụng biểu thức tính thế năng trọng trường:
Cách giải:
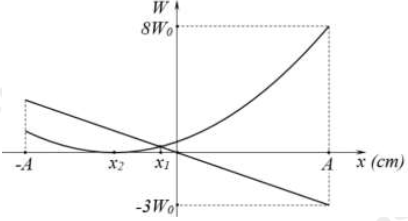
Từ đồ thị, ta thấy thế năng đàn hồi cực tiểu = 0 tại x2 \( \Rightarrow \) đây chính là độ dãn của lò xo tại VTCB
Lại có:
+ Thế năng đàn hồi: \({{\rm{W}}_{{\rm{d}}h}} = \frac{1}{2}k{\left( {x - {x_2}} \right)^2}\)
+ Thế năng trọng trường:
Từ đồ thị:
+ Xét tại
Theo đề bài ta có: \({x_1} - {x_2} = 3,66\;{\rm{cm}} \Rightarrow \) thay vào (*) ta suy ra:
+ Xét tại
Thay số vào ta suy ra:\(\frac{8}{{ - 3}} = \frac{{{{(A + 4,9997)}^2}}}{{2 \cdot A( - 4,9997)}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{A = 14,9991\;{\rm{cm}}}\\{A = 1,667\;{\rm{cm}}}\end{array}} \right.\)
Chọn B.
