Tìm số tự nhiên x, biết:

a) 2^x + 12 = 44;

b) 2.5^x+1 – 1.100 = 6.5²;

c) 2.3^x+1 = 10.3¹² + 8.3¹²;

d) 2^x + 2^x+3 = 144.

Rút gọn biểu thức sau:

a) A = 1 + 3 + 3² + 3³ + … + 3⁹⁹ + 3¹⁰⁰;

b) B = 2¹⁰⁰ – 2⁹⁹ + 2⁹⁸ – 2⁹⁷ + … - 2³ + 2² – 2 + 1.

a) Viết mỗi số sau thành bình phương của một số tự nhiên:

36; 64; 169; 225; 361; 10 000.

b) Viết mỗi số sau thành lập phương của một số tự nhiên:

8; 27; 125; 216; 343; 8 000.

a) Cho A = 4 + 2² + 2³ + … +2²⁰⁰⁵. Chứng tỏ rằng A là một lũy thừa cơ số 2.

b) Cho B = 5 + 5² + 5³ + … + 5²⁰²¹. Chứng tỏ B + 8 không thể là bình phương của một số tự nhiên.

 So sánh:

a) 2²⁰⁰ .2¹⁰⁰ và 3¹⁰⁰.3¹⁰⁰;

b) 21¹⁵ và 27⁵.49⁸;

c) 3³⁹ và 11².

So sánh:

a) 2⁶ và 6²;

b) 7³⁺¹ và 7³ + 1;

c) 13¹⁴ – 13¹³ và 13¹⁵ – 13¹⁴;

d) 3²⁺ⁿ và 2³⁺ⁿ.

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

a) 7⁴.7⁵.7⁶;

b) (54 : 3)⁷.324;

c) [(8 + 2)².10¹⁰⁰] : (10⁰.10⁹⁴);

d) a⁹:a⁹ (a 0).

a) Viết các số 123; 2 355; $\overline{\mathrm{abcde}}$ dưới dạng tổng các lũy thừa của 10.

b) Tìm số $\overline{\mathrm{abcdef}} (\mathrm{d}\ne 0)$ sao cho $\overline{\mathrm{abcdef}} = 999.\overline{\mathrm{abc}} +200$

Tìm chữ số tận cùng của kết quả mỗi phép tính sau:

a) 54¹⁰;

b) 49¹⁵;

c) 11²⁰ + 119²¹ + 2 000²²;

d) 138³³ – 2 020¹⁴.

Tế bào lớn lên đến một kích thước nhất định thì phân chia. Quá trình đó diễn ra như sau: Đầu tiên từ 1 nhân thành 2 nhân tách xa nhau. Sau đó chất tế bào được phân chia, xuất hiện một vách ngăn, ngăn đôi tế bào cũ thành 2 tế bào con. Các tế bào con tiếp tục lớn lên cho đến khi bằng tế bào mẹ. Các tế bào này tiếp tục phân chia thành 4, rồi thành 8, … tế bào.

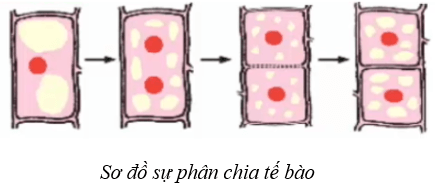
Như vậy từ một tế bào mẹ: sau khi phân chia lần 1 được hai tế bào con; lần hai được 2² = 4 (tế bào con); lần ba được 2³ = 8 (tế bào con). Hãy tính số tế bào con có được ở lần phân chia thứ 5, thứ 8 và thứ 11.

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa, một tích các lũy thừa hoặc một tổng các lũy thừa:

a) 3.3.3.3.3;

b) y.y.y.y;

c) 5.p.5.p.2.q.4.q;

d) a.a + b.b + c.c.c + d.d.d.d.

Một nền nhà có dạng hình vuông gồm a hàng, mỗi hàng lát a viên gạch. Ban An đếm được 113 viên gạch được lát trên nền nhà đó. Theo em bạn An đếm đúng hay sai? Vì sao?

Cho các số 16; 20; 25; 60; 81; 90; 1 000; 1 331. Trong các số đó, số nào viết được dưới dạng lũy thừa của một số tự nhiên với số mũ lớn hơn 1? (Chú ý rằng có những số có nhiều cách viết dưới dạng lũy thừa).