Trong tất cả các cặp \(\left( {x;y} \right)\) thỏa mãn \({\log _{{x^2} + {y^2} + 2}}\left( {2x - 4y + 6} \right) \ge 1\). Tìm \(m\) để tồn tại duy nhất một cặp \(\left( {x;y} \right)\) sao cho \({x^2} + {y^2} + 2x - 2y + 2 - m = 0\).
A. \(\sqrt {13} - 3\) và \(\sqrt {13} - 3\).
B. \(\sqrt {13} - 3\).
C. \({\left( {\sqrt {13} - 3} \right)^2}\).
D. \({\left( {\sqrt {13} - 3} \right)^2}\) và \({\left( {\sqrt {13} + 3} \right)^2}\).
Giải bởi Vietjack
Ta có: \({\log _{{x^2} + {y^2} + 2}}\left( {2x - 4y + 6} \right) \ge 1 \Leftrightarrow 2x - 4y + 6 \ge {x^2} + {y^2} + 2 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} \le 9\,\,\,\,\,\left( 1 \right)\)
Giả sử \(M\left( {x;y} \right)\) thỏa mãn \(\left( 1 \right)\), khi đó tập hợp điểm \(M\) là hình tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {1; - 2} \right)\) và bán kính \({R_1} = 3\)
Ta có: \({x^2} + {y^2} + 2x - 2y + 2 - m = 0 \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = m\,\,\,\,\,\left( 2 \right)\)
Nếu \(m < 0\) suy ra \(\left( 2 \right)\) vô nghiệm, do đó \(m < 0\) không thỏa mãn.
Nếu \(m = 0\) suy ra \(\left( 2 \right) \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\), không thỏa mãn \(\left( 1 \right)\).
Nếu \(m >0\) khi đó \(\left( 2 \right)\) là đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( { - 1;1} \right)\) và bán kính \({R_2} = \sqrt m \)
Ta có \({I_1}{I_2} = \sqrt {13} >{R_1} \Rightarrow {I_2}\) nằm ngoài đường tròn \(\left( {{C_1}} \right)\). Vậy để tồn tại duy nhất một cặp \(\left( {x;y} \right)\)thỏa mãn đề bài khi và chỉ khi \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc ngoài hoặc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc trong.
\( \Leftrightarrow \left[ \begin{array}{l}{I_1}{I_2} = {R_1} + {R_2}\\{I_1}{I_2} = {R_2} - {R_1}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt {13} = 3 + \sqrt m \\\sqrt {13} = \sqrt m - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = {\left( {\sqrt {13} - 3} \right)^2}\\m = {\left( {\sqrt {13} + 3} \right)^2}\end{array} \right.\)
Chọn đáp án D
</>
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian \[Oxyz\] cho tam giác \[ABC\] có \[A(2;\,2;\,0)\], \[B(1;\,0;\,2)\], \[C(0;\,4;\,4)\]. Viết phương trình mặt cầu có tâm là \(A\) và đi qua trọng tâm \[G\] của tam giác \(ABC\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^2 {f\left( x \right)} \,{\rm{d}}x = 9;\int\limits_2^4 {f\left( x \right)\,} {\rm{d}}x = 4\). Tính \(I = \int\limits_0^4 {f\left( x \right)} \,{\rm{d}}x\)?
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang vuông tại \[A;\;B\]. Gọi \[G\] là trọng tâm tam giác \[SAB\]. Biết \[SA = a\sqrt 6 \] và vuông góc với mặt đáy \[(ABCD)\],\[AB = BC = \frac{1}{2}AD = a\]. Tính theo \[a\] khoảng cách từ \[G\] đến mặt phẳng \[\left( {SCD} \right)\].
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y - z = 0\) và mặt phẳng \(\left( Q \right):2x - y + z = 0\). Giao tuyến của mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có phương trình là
Trong không gian \[Oxyz\], cho mặt phẳng\((\alpha ):2x + y - z + 1 = 0\). Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng \[(\alpha )\]?
Đường thẳng đi qua điểm \(M\left( {3;2;1} \right)\) và vuông góc với mặt phẳng \(\left( P \right):2x - 5y + 4 = 0\) có phương trình là
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \({u_5} = 10\). Tính tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\).
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Tìm tọa độ điểm biểu diễn số phức \(\frac{{7 - 4i}}{{{z_1}}}\) trên mặt phẳng phức?
Tập xác định của hàm số \(y = {\log _5}\left( {2x + 1} \right)\) là
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ.
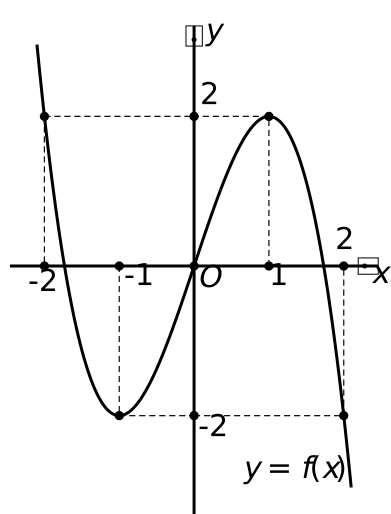
Phương trình \[f\left( {2\cos x} \right) = 2\] có bao nhiêu nghiệm \[x \in \left[ {0;3\pi } \right]\]?
Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số dưới đây ?
Hỏi có bao nhiêu cách xếp bốn bạn An, Bình, Cường, Dũng ngồi vào một bàn học gồm bốn chỗ?
Thể tích khối lăng trụ có chiều cao bẳng \(2\) và diện tích đáy bằng \(6\) là
Trong không gian \[Oxyz\], mặt phẳng \[\left( {Oyz} \right)\]có phương trình là
