Cho hình lăng trụ đứng \[{\mkern 1mu} ABCD.A'B'C'D'\] có đáy là hình thoi có cạnh \[4a\], \[A'A = 8a\], \[\widehat {BAD} = {120^{0.}}\]. Gọi \[M,N,K\] lần lượt là trung điểm cạnh \[AB',B'C,BD'\]. Thể tích khối da diện lồi có các đỉnh là các điểm \[A,B,C,M,N,K\] là:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
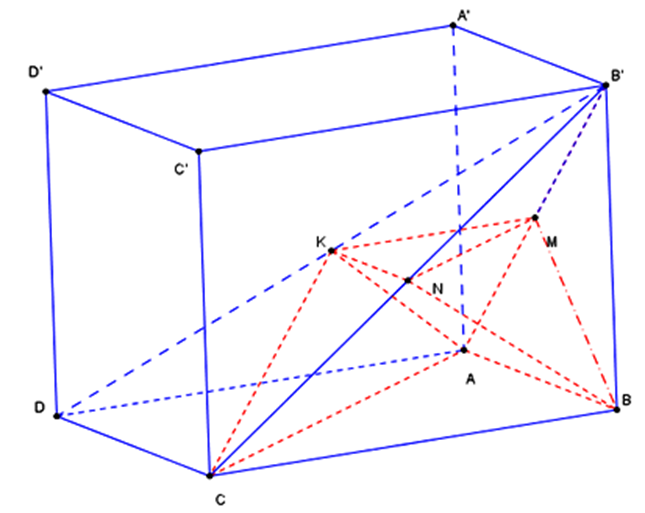
\({\rm{MN // AC}};{\rm{ MN}} = \frac{1}{2}AC,{\rm{ MNCA}}\) là hình thang.
\({V_{MNK{\rm{A}}BC}} = {V_{K.MNCA}} + {V_{B.MNCA}}\)
DK cắt \(\left( {B'AC} \right)\) tại \(B'\), \(\frac{{B'K}}{{B'D}} = \frac{1}{2} \Rightarrow \frac{{d\left( {K;(MNC{\rm{D}})} \right)}}{{d\left( {D;(MNCA)} \right)}} = \frac{1}{2} \Rightarrow {V_{K.MNCA}} = \frac{1}{2}{V_{D.MNCA}}\)
Mà: \({V_{B.MNCA}} = {V_{D.MNCA}}\) nên ta có: \({V_{MNK{\rm{A}}BC}} = \frac{1}{2}{V_{B.MNCA}} + {V_{B.MNCA}} = \frac{3}{2}{V_{B.MNCA}}\)
Mặt khác: \({S_{MNCA}} = \frac{3}{4}{S_{B'AC}} \Rightarrow {V_{B.MNCA}} = \frac{3}{4}{V_{B.B'AC}} = \frac{3}{4}{V_{B'.ABC}} = \frac{3}{4}.\frac{1}{6}{V_{ABCD.A'B'C'D'}} = 8\sqrt 3 {a^3}\)
\({V_{MNKABC}} = \frac{3}{2}{V_{B.MNCA}} = \frac{3}{2}8\sqrt 3 {\mkern 1mu} {a^3} = 12\sqrt 3 {\mkern 1mu} {a^3}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một hộp chứa 4 quả cầu màu đỏ, 5 quả cầu màu xanh và 7 quả cầu màu vàng. Lấy ngẫu nhiên cùng lúc ra 4 quả cầu từ hộp đó. Tính xác suất sao cho 4 quả cầu được lấy ra có đúng một quả cầu màu đỏ và không quá hai quả cầu màu vàng.
Tìm hệ số của số hạng chứa \[{x^3}\] trong khai triển biểu thức \[P = {x^2}{\left( {2x + 1} \right)^{10}} - {\left( {x - 2} \right)^8}\]
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \[x = 0\] và \[x = 2\sqrt 3 ,\] biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\left( {0 \le x \le 2\sqrt 3 } \right)\] thì thiết diện là một hình tam giác đều có cạnh là \[x\sqrt 2 .\]
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10;10} \right]\] để bất phương trình sau nghiệm đúng \[\forall x \in \mathbb{R}:{\left( {6 + 2\sqrt 7 } \right)^x} + \left( {2 - m} \right){\left( {3 - \sqrt 7 } \right)^x} - \left( {m + 1} \right){2^x} \ge 0\]?
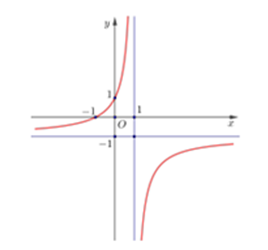
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số cho dưới đây?
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \[v\left( t \right) = 10t - {t^2},\] trong đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, \[v\left( t \right)\] được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt đấy và \[SC = a\sqrt 3 \]. Thể tích của khối chóp đã cho bằng
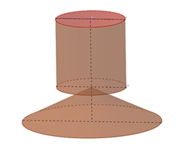
Một khối đồ chơi gồm một khối hình trụ (T) gắn chồng lên một khối hình nón (N), lần lượt có bán kính đáy và chiều cao tương ứng là \[{r_1},{h_1},{r_2},{h_2}\] thỏa mãn \[{r_2} = 2{r_1},{h_1} = 2{h_2}\] (hình vẽ). Biết rằng thể tích của khối nón (N) bằng \[20{\rm{c}}{{\rm{m}}^{\rm{3}}}\]. Thể tích của toàn bộ khối đồ chơi bằng
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \[A\left( {1; - 1;2} \right)\] và có một vectơ pháp tuyến \[\vec n = \left( {2;2; - 1} \right).\] Phương trình của (P) là
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a, SA vuông góc với đáy, \[SB = 5a\]. Tính sin của góc giữa cạnh SC và mặt đáy \[\left( {ABCD} \right)\].
Trong mặt phằng cho 10 điểm phân biệt. Số vectơ khác \[\overrightarrow 0 \], có điểm đầu và điểm cuối lấy trong các điểm đã cho là
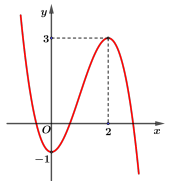
Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\left( {a,b,c,d \in \mathbb{R}} \right)\] có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình \[2f\left( {\left| x \right|} \right) - m = 0\] có đúng bốn nghiệm thực phân biệt.
Tập hợp điểm biểu diễn số phức z biết \[\left| {z - \left( {3 - 4i} \right)} \right| = 2.\]