Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích \[100{\mkern 1mu} c{m^3}\]. Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất.

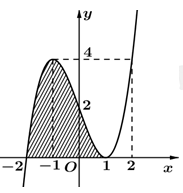
Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm số bậc ba \[y = a{x^3} + b{x^2} + cx + d\] và trục hoành.

Cho tập hợp \[A = \left\{ {2;3;4;5;6;7;8} \right\}.\] Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số trong tập A. Chọn ngẫu nhiên một chữ số từ S. Xác suất để số được chọn mà trong mỗi số luôn luôn có mặt hai chữ số chẵn và hai chữ số lẻ là

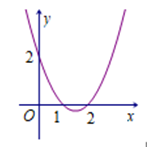
Cho hàm số \[y = f\left( x \right)\]. Hàm số \[y = f'\left( x \right)\] có đồ thị là đường parabol như hình bên. Hàm số \[y = f\left( {1 - {x^2}} \right) + 2{x^2}\] nghịch biến trên khoảng nào dưới đây?

Cho số phức \[z = a + bi\left( {a,b \in \mathbb{R}} \right)\] thỏa mãn \[z + 7 + i - \left| z \right|\left( {2 + i} \right) = 0\] và \[\left| z \right| < 3.\] Tính giá trị \[P = a + b.\]

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm \[I\left( {1;2; - 4} \right)\] và diện tích của mặt cầu đó bằng \[36\pi .\]

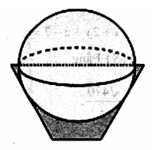
Một cái thùng đựng đầy nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng ba lần bán kính mặt đáy của thùng. Người ta thả vào đó một khối cầu có đường kính bằng \[\frac{3}{2}\] chiều cao của thùng nước và đo được thể tích nước tràn ra ngoài là \[54\sqrt 3 \pi \left( {d{m^3}} \right).\] Biết rằng khối cầu tiếp xúc với mặt trong của thùng và đúng một nửa của khối cầu đã chìm trong nước (hình vẽ). Thể tích nước còn lại trong thùng có giá trị nào sau đây?

Cho hình chóp S.ABC có tam giác ABC vuông tại A, \[AB = 2a\], \[AC = 3a\], SA vuông góc với đáy và \[SA = a\]. Thể tích khối chóp S.ABC bằng

Cho hàm số \[y = f\left( x \right)\] liên tục và có đạo hàm trên đoạn \[\left[ { - \frac{1}{2};\frac{1}{2}} \right]\] thỏa mãn \[\int\limits_{\frac{{ - 1}}{2}}^{\frac{1}{2}} {\left[ {{f^2}\left( x \right) - 2f\left( x \right).\left( {3 - x} \right)} \right]{\rm{d}}x} = \frac{{ - 109}}{{12}}.\] Tính tích phân \[I = \int\limits_0^{\frac{1}{2}} {\frac{{f\left( x \right)}}{{{x^2} - 1}}{\rm{d}}x} .\]

Trong không gian Oxyz, cho đường thẳng \[d:\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z - 1}}{1}\] và mặt cầu \[(S):{\left( {x - 4} \right)^2} + {\left( {y - 5} \right)^2} + {\left( {z - 7} \right)^2} = 2.\] Hai điểm \[A,B\] thay đổi trên (S) sao cho tiếp diện của (S) tại A và B vuông góc với nhau. Đường thẳng qua A song song với d cắt mặt phẳng \[(Oxy)\] tại M, đường thẳng qua B song song với d cắt mặt phẳng \[(Oxy)\] tại N. Tìm giá trị lớn nhất của tổng \[AM + BN.\]

Một hình trụ có bán kính đáy và chiều cao đều bằng 4 dm. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng (ABCD) không vuông góc với mặt đáy của hình trụ. Tính diện tích S của hình vuông \[ABCD.\]

Số tiệm cận đứng của đồ thị hàm số \[y = \frac{{\sqrt {2x + 1} - 3}}{{{x^2} - 16}}\] là

Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[A\left( {3;2; - 3} \right),{\mkern 1mu} B\left( { - 1;2;2} \right),{\mkern 1mu} C\left( {4; - 1; - 2} \right).\] Tìm tọa độ trọng tâm G của tam giác \[ABC.\]

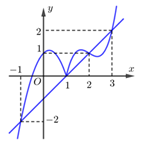
Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\] có \[f\left( { - 3} \right) > 8,\;f\left( 4 \right) > \frac{9}{2},f\left( 2 \right) < \frac{1}{2}.\] Biết rằng hàm số \[y = f'\left( x \right)\] có đồ thị như hình vẽ. Số điểm cực trị của hàm số \[y = \left| {2f\left( x \right) - {{\left( {x - 1} \right)}^2}} \right|\] là

Cho phương trình \[{\log _3}\frac{{2{x^2} - x + m}}{{{x^2} + 1}} = {x^2} + x + 4 - m.\] Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 2018;2018} \right]\] để phương trình có hai nghiệm trái dấu?

Cho hình chóp S.ABCD có SA vuông góc với đáy và \[SA = a\sqrt 3 ,\] đáy ABCD là hình vuông cạnh 2a. Gọi E là trung điểm của cạnh AD. Khoảng cách giữa SC và BE là