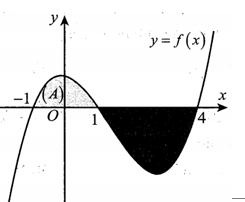
Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng (A),(B) lần lượt bằng 3 và 7. Tích phân bằng:
A.
B. 2
C.
D. -2
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Đặt .
Đổi cận .
Khi đó .
Mặt khác . Vậy .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 lập các số tự nhiên có tám chữ số đôi một khác nhau. Lấy ngẫu nhiên một số vừa lập. Xác suất để lấy được số chia hết cho 1111 là:
Cho hàm số y=f(x) có bảng biến thiên như sau:
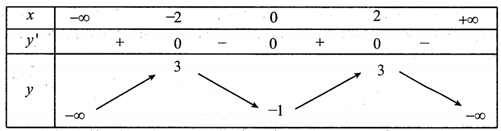
Số điểm cực đại của hàm số đã cho bằng:
Cho F(x) là một nguyên hàm của f(x) trên [0;1], biết và . Giá trị tích phân là:
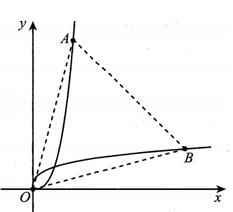
Cho các hàm số và cùng xét trên có đồ thị như hình vẽ bên. Gọi các điểm A và B lần lượt nằm trên các đồ thị đó sao cho AOB là tam giác đều. Biết rằng tồn tại hai tam giác như vậy với diện tích lần lượt là và trong đó . Tỷ số bằng:
Có 12 bạn học sinh trong đó có đúng một bạn tên A và đúng một bạn tên B. Xếp ngẫu nhiên 12 học sinh vào một bàn tròn và một bàn dài mỗi bàn 6 học sinh. Xác suất để hai bạn A và B ngồi cùng bàn và cạnh nhau bằng:
Cho mặt cầu và một điểm A với . Từ A dựng các tiếp tuyến với mặt cầu , gọi M là tiếp điểm bất kì. Tập hợp các điểm M là:
Cho hàm số . Giả sử A, B là các điểm cực trị của đồ thị hàm số. Biết rằng AB đi qua gốc tọa độ. Giá trị nhỏ nhất của biểu thức là:
Cho hàm số y=f(x) có bảng biến thiên như sau:
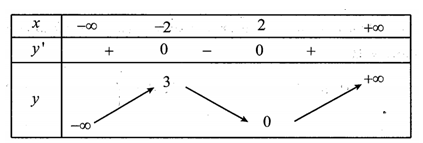
Đồ thị hàm số có bao nhiêu tiệm cận đứng?
Trong không gian Oxyz, cho điểm và mặt cầu . Từ điểm A kẻ 3 tiếp tuyến AB, AC, AD với mặt cầu (S), trong đó B, C, D là các tiếp điểm. Phương trình mặt phẳng (BCD) là:
Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’, là thể tích tứ diện A’ABD. Hệ thức nào sau đây đúng?