Cho hình hộp ABCD.A’B’C’D’ có đáy là hình thoi cạnh a và . Mặt chéo ACC’A’ nằm trong mặt phẳng vuông góc với đáy, đồng thời ACC’A’ cũng là hình thoi có . Thể tích khối tứ diện ACB’D’ là:
A.
B.
C.
 Giải bởi Vietjack
Giải bởi Vietjack
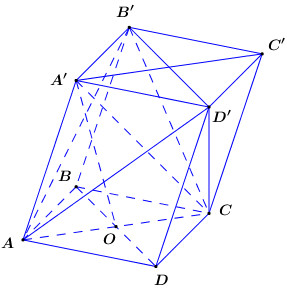
Gọi ⇒O là trung điểm của AC và BD.
Vì ACC’A’ là hình thoi nên AA’ = AC, lại có (gt) nên là tam giác đều
Ta có: \[\left\{ {\begin{array}{*{20}{l}}{\left( {ACC'A'} \right) \bot \left( {ABCD} \right) = AC}\\{A'O \subset \left( {ACC'A'} \right),{\mkern 1mu} {\mkern 1mu} A'O \bot AC}\end{array}} \right. \Rightarrow A'O \bot \left( {ABCD} \right)\].
Xét tam giác ABC có: AB = AD (do ABCD là hình thoi), nên tam giác ABC đều cạnh a.
và .
là tam giác đều cạnh .
Vậy \[{V_{ACB'D'}} = \frac{1}{3}{V_{ABCD.A'B'C'D'}} = \frac{1}{3}.A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{3a}}{2}.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{4}\].
Đáp án B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả các điểm M nằm trên đồ thị hàm số mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng .
Cho hình chóp S.ABC, đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt đáy. Biết SA = AB = BC và diện tích mặt cầu ngoại tiếp hình chóp bằng . Thể tích khối chóp là:
Cho hình lăng trụ đều ABC.A’B’C’, tất cả các cạnh có độ dài bằng a. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM và BC’.
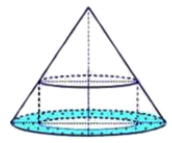
Cho một hình trụ thay đổi nội tiếp trong một hình nón cố định cho trước (tham khảo hình vẽ bên). Gọi thể tích các khối nón và khối trụ tương ứng là V và V’. Biết rằng V’ là giá trị lớn nhất đạt được, khi đó tỉ số \[\frac{{V'}}{V}\] bằng:
Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm . Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.
Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.
Cho hình lăng trụ đứng ABC.A’B’C’. Đáy là tam giác vuông tại A, có BC = 2AC = 2a. Đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng;
Cho một hình nón đỉnh S đáy là đường tròn (O), bán kính đáy bằng 1. Biết thiết diện qua trục là một tam giác vuông. Tính diện tích xung quanh của hình nón.
Cho tứ diện ABCD có ABC, ABD, ACD là các tam giác vuông tương ứng tại A, B, C. Góc giữa AD và (ABC) bằng , và khoảng cách giữa AD và BC bằng a. Tính thể tích khối tứ diện ABCD.