Cho hai hàm số \(y = x(x - 2)(x - 3)(m - |x|);y = {x^4} - 6{x^3} + 5{x^2} + 11x - 6\) có đồ thị lần lượt là \(\left( {{C_1}} \right),\left( {{C_2}} \right)\). Có bao nhiêu giá trị nguyên \(m\) thuộc đoạn \([ - 2020;2020]\) để \(\left( {{C_1}} \right)\) cắt \(\left( {{C_2}} \right)\) tại 4 điểm phân biệt?
A. \(2021\)
B. \(2019\)
C. \(4041\)
D. \(2020\)
Giải bởi Vietjack
Xét phương trình hoành độ giao điểm:
\(x\left( {x - 2} \right)\left( {x - 3} \right)\left( {m - \left| x \right|} \right) = {x^4} - 6{x^3} + 5{x^2} + 11x - 6{\rm{ }}\left( 1 \right)\)
Số giao điểm của \(\left( {{C_1}} \right);\left( {{C_2}} \right)\) là số nghiệm của phương trình \(\left( 1 \right).\)
Do \(x = 0;x = 2;x = 3\) không là nghiệm của phương trình (1) nên:
\(\left( 1 \right) \Leftrightarrow \frac{{{x^4} - 6{x^3} + 5{x^2} + 11x - 6}}{{x\left( {x - 2} \right)\left( {x - 3} \right)}} = m - \left| x \right|\)
\( \Leftrightarrow x - 1 - \frac{2}{{x - 2}} - \frac{3}{{x - 3}} - \frac{1}{x} + \left| x \right| = m\)
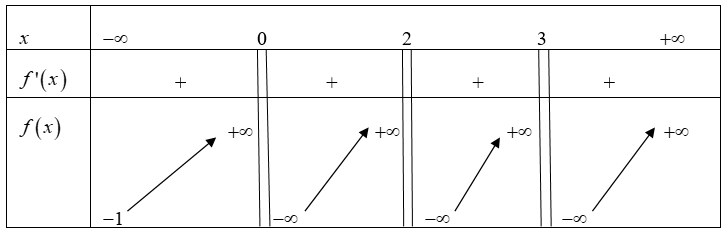
Đặt \(f\left( x \right) = x - 1 - \frac{2}{{x - 2}} - \frac{3}{{x - 3}} - \frac{1}{x} + \left| x \right| = \left\{ \begin{array}{l}2x - 1 - \frac{2}{{x - 2}} - \frac{3}{{x - 3}} - \frac{1}{x},x >0\\ - 1 - \frac{2}{{x - 2}} - \frac{3}{{x - 3}} - \frac{1}{x},x < 0\end{array} \right.\)
Ta có \(f'\left( x \right) = \left\{ \begin{array}{l}2 + \frac{2}{{{{\left( {x - 2} \right)}^2}}} + \frac{3}{{{{\left( {x - 3} \right)}^2}}} + \frac{1}{{{x^2}}},x \ge 0\\\frac{2}{{{{\left( {x - 2} \right)}^2}}} + \frac{3}{{{{\left( {x - 3} \right)}^2}}} + \frac{1}{{{x^2}}},x < 0\end{array} \right. \Rightarrow f'\left( x \right) >0,\forall x \in \mathbb{R}.\)</>
Suy ra \(f\left( x \right)\) đồng biến trên từng khoảng xác định của nó: \(\left( { - \infty ;0} \right);\left( {0;2} \right);\left( {2;3} \right);\left( {3; + \infty } \right).\)
Mặt khác \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = - \infty \)
Bảng biến thiên
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật với \[AB = 2a\], \[BC = a\sqrt 3 \]. Cạnh bên \[SA\] vuông góc với đáy và đường thẳng \[SC\] tạo với mặt phẳng \[\left( {SAB} \right)\] một góc \[30^\circ \]. Tính thể tích \[V\] của khối chóp \[S.ABCD\] theo \[a\].
Số nghiệm của phương trình\(\frac{{\sin 2x}}{{\cos x + 1}} = 0\) trên đoạn \(\left[ {0;2020\pi } \right]\) là
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình chữ nhật \(AB = a;AD = 4a;SA = a\sqrt {15} \),\(SA \bot \left( {ABCD} \right)\) , \(M\) là trung điểm của \(AD\) , \(N\) thuộc cạnh \(BC\) sao cho \(BC = 4BN\) . Khoảng cách gữa \(MN\) và \(SD\) là
Gọi \(l,h,R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích toàn phần Stp của hình trụ (T) là:
Cho mặt cầu \(\left( S \right)\) có tâm \(O\), bán kính \(6\).Biết khoảng cách từ tâm O đến mặt phẳng \(\left( \alpha \right)\) bằng \(4\). Mặt phẳng \(\left( \alpha \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có bán kính bằng
Gọi S là tập các giá trị m nguyên\(m\) để phương trình \(9.{\left( {\sqrt {10} + 3} \right)^x} + {\left( {\sqrt {10} - 3} \right)^x} - m + 2020 = 0\) có đúng hai nghiệm âm phân biệt. Số tập con của S là
Một khối nón có đường sinh bằng 2a và diện tích xung quanh của mặt nón bằng . Tính thể tích của khối nón đã cho?
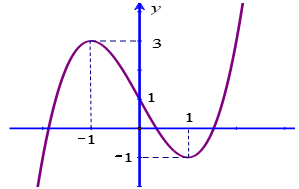
Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?
Gọi S là tập giá trị nguyên \(m \in \left[ { - 2020;2020} \right]\) để phương trình \(2{\sin ^2}x + m\sin 2x = 2m\) vô nghiệm.Tính tổng các phần tử của S
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 11 = 0\). Tìm bán kính của đường tròn \((C')\) là ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm Otỉ số \(k = - 2020\) và phép tịnh tiến theo véctơ \(\overrightarrow v = (2019;2020)\)là:
Cho tập hợp A gồm có 2021 phần tử. Số tập con của A có số phần tử \( \ge 1011\) bằng
Số nghiệm của phương trình \[{\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2}\] là
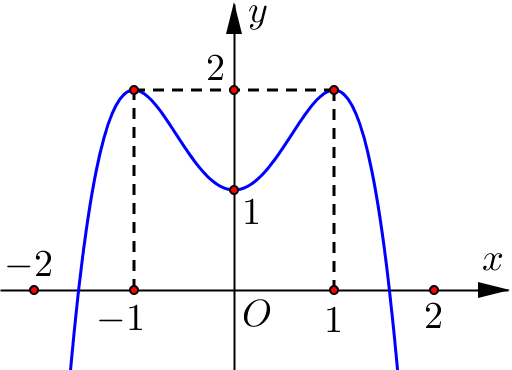
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của tham số m để phương trình \(\left| {f\left( {\cos x} \right)} \right| = - 2m + 3\) có 4 nghiệm thuộc khoảng là
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(3a\). Gọi \(M\)thuộc cạnh \(B'C'\) sao cho \(MC' = 2MB'\) , \(N\) thuộc cạnh \(AC\) sao cho \(AC = 4NC\) Mặt phẳng \(\left( {A'MN} \right)\) cắt cạnh \(BC\) tại \(Q\). Tính thể tích \(V\) khối đa diện \(CNQ.C'A'M\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi \(AC = 2a;\,BD = 3a\), \(SA = a\), \(SA\) vuông góc với mặt đáy. Thể tích của khối chóp \(S.ABCD\) là
