Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(5; 0; 0) và B(3; 4; 0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
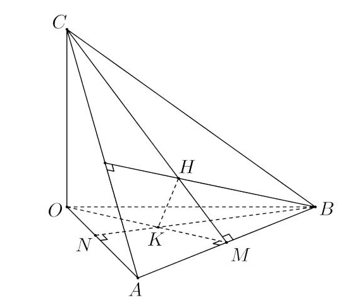
Ta có suy ra
Mà cân tại O.
Gọi M là trung điểm của AB, K là trực tâm của tam giác OAB
Suy ra và
Ta có (do ) (1).
Mặt khác
Mà (do H là trực tâm của ) suy ra
Từ (1) và (2) suy ra vuông tại H.
Vì M, K (OCM) cố định và nên H thuộc đường tròn đường kính KM.
Gọi N là hình chiếu của B lên trục Ox suy ra N(3; 0; 0)
Từ đó ta tính được NA = 2, BN = 4 và
Ta có đồng dạng (g.g) nên suy ra
Vậy khi C di động trên trục Oz thì H luôn thuộc đường tròn cố định có bán kính bằng
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi R, S, V lần lượt là bán kính, diện tích mặt cầu và thể tích của khối cầu. Công thức nào sau đây sai?
Hàm số (tham số m, n) đồng biến trên khoảng Giá trị nhỏ nhất của biểu thức bằng
Cho khối lăng trụ có diện tích đáy bằng và khoảng cách giữa hai đáy bằng 3a. Tính thể tích V của khối lăng trụ đã cho.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng
Tổng bình phương các giá trị của tham số m để đường thẳng cắt đồ thị tại hai điểm phân biệt A, B với là
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm trong đó Mặt phẳng (ABC) đi qua điểm I(1; 2; 3) sao cho thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
Cổng trường Đại học Bách Khoa Hà Nội có hình dạng Parabol, chiều rộng 8m, chiều cao 12,5m. Diện tích của cổng là:
Biết số phức z thỏa mãn và biểu thức đạt giá trị lớn nhất. Tính |z|.