Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, cạnh bên SD vuông góc với mặt phẳng đáy. Cho biết AB=AD=a,CD=2a, góc giữa hai mặt phẳng (SAB) và (SBC) bằng 300. Tính thể tích khối chóp đã cho.
A. 2a3
B. a3
C. 3a32
D. a32
Giải bởi Vietjack
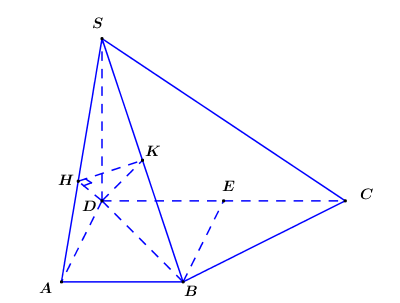
Trong (SAD) kẻ DH⊥SA(H∈SA), trong (SBD) kẻ DK⊥SB(K∈SB).
Ta có:
{SA⊥ADAB⊥SD⇒AB⊥(SAD)⇒AB⊥DH
{DH⊥ABDH⊥SA⇒DH⊥(SAB)(1)
Gọi E là trung điểm của CD⇒ABED là hình vuông nên BE=AD=a=12CD⇒ΔBCD vuông tại B.
Ta có:
{BC⊥BDBC⊥SD⇒BC⊥(SBD)⇒BC⊥DK
{DK⊥BCDK⊥SB⇒DK⊥(SBC)(2)
Từ (1) và (2)⇒∠((SAB);(SBC))=∠(DH;DK)=300
Mà DH⊥(SAB)⇒DH⊥HK⇒ΔDHK vuông tại H⇒∠HDK=300
Đặt SD = x (x > 0) áp dụng hệ thức lượng trong tam giác vuông ta có:
DH=AD.SD√AD2+SD2=a.x√a2+x2
DK=BD.SD√BD2+SD2=a√2.a√2a2+x2
Xét tam giác vuông DHK ta có: cos∠HDK=DHDK⇒ax√a2+x2:a√2x√2a2+x2=√32
⇔√2a2+x2√2a2+2x2=√32
⇔4(2a2+x2)=3(2a2+2x2)
⇔8a2+4x2=6a2+6x2
⇔2a2=2x2⇔x=a
Ta có SABCD=12(AB+CD).AD=12(a+2a).a=3a22.
Vậy VS.ABCD=13SD.SABCD=13.a.3a22=a32.
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tổ gồm 6 học sinh trong đó có An và Hà được xếp ngẫu nhiên ngồi vào một dãy 6 cái ghế, mỗi người ngồi một ghế. Tính xác suất để An và Hà không ngồi cạnh nhau
Có bao nhiêu số nguyên dương a sao cho tồn tại số thực b thỏa mãn 2a=3b và a - b < 4
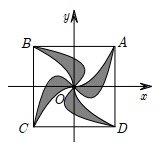
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ toạ độ Oxy với O là tâm hình vuông sao cho A(1; 1) như hình vẽ bên thì các đường cong OA có phương trình y=x2 và y=ax3+bx. Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm 13 diện tích mặt sàn.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a√3,BC=a, các cạnh bên của hình chóp bằng a√5. Gọi M là trung điểm SC. Tính khoảng cách từ M đến mặt phẳng (ABCD).
Cho hàm số f(x) liên tục trên ℝ và có bảng xét dấu đạo hàm như hình vẽ.
Hàm số đã cho có bao nhiêu điểm cực đại?
Khối lăng trụ có chiều cao bằng h và diện tích đáy bằng S thì có thể tích bằng
Cho hàm số y = f(x) có đạo hàm, đồng biến và nhận giá trị âm trên (0;+∞). Hàm số g(x)=f(x)x có bao nhiêu điểm cực trị trên (0;+∞).?
Cho tứ diện ABCD có AB = 2a, độ dài tất cả các cạnh còn lại cùng bằng a√2. Diện tích của mặt cầu ngoại tiếp tứ diện đã cho bằng
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số đã cho trên [-1; 1] là:
