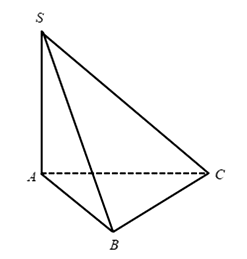
A. √6a336.
B. √6a312.
C. √2a312.
D. √6a34.
Giải bởi Vietjack
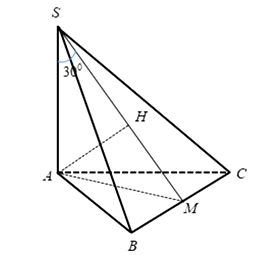
Gọi M là trung điểm của BC. Nối SM kẻ AH vuông góc với SM tại H
Ta có:
BC⊥AM (do M là trung điểm của BC và tam giác ABC vuông cân tại A)
BC⊥SA (do SA⊥(ABC),BC⊂(ABC))
Nên: BC⊥(SAM)⇒BC⊥AH (vì AH⊂(SAM))
Lại có: AH⊥SM (cách dựng)
Suy ra: AH⊥(SBC) tại H
⇒H là hình chiếu của A trên (SBC).
⇒SH là hình chiếu của SA trên (SBC).
⇒^(SA,(SBC))=^(SA,SH)=^ASH=^ASM⇒^ASM=300
+) Tam giác ABC vuông cân tại A⇒2AB2=BC2=2a2⇒AB=a⇒AC=AB=a
⇒SABC=12AB.AC=a22
Có: AM=12BC=a√22
Tam giác SAM vuông tại A⇒SA=AMtan300=a√62
Vậy thể tích của khối chóp S.ABC là: VS.ABC=13.SA.SABC=13.a√62.a22=a3√612.
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):(x−3)2+(y−2)2+(z−1)2=3 có tâm I và đường thẳng d:x−12=y+63=z+22. Gọi A là điểm nằm trên đường thẳng d. Từ A kẻ các tiếp tuyến AB, AC, AD đến mặt cầu (S) với B, C, D là các tiếp điểm. Khi thể tích khối chóp I.BCD đạt giá trị lớn nhất, mặt phẳng (BCD) có phương trình là mx+ny+pz+12=0. Giá trị của m + n + p bằng
Cho F(x) là một nguyên hàm của hàm số f(x) = 4x + cos2x thỏa mãn F(0) = 1. Giá trị F(π) bằng
Trong không gian Oxyz, cho mặt cầu (S):x2+y2+z2−8x+2y+1=0. Tâm của mặt cầu (S) có tọa độ là
Trong không gian Oxyz, cho điểm A(0; -1; -6) và đường thẳng d:x−42=y−21=z+11−6. Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến mặt phẳng (P) lớn nhất. Khoảng cách từ điểm M(5; 1; 1) đến mặt phẳng (P) bằng
Cho hàm số f(x) = sinx - 1. Trong các khẳng định sau, khẳng định nào đúng?
Thể tích V của khối trụ có chiều cao h = 3cm bán kính r = 2cm bằng
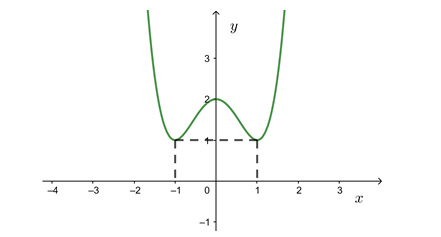
Cho hàm số f(x)=ax−2bx+c với a,b,c∈ℝ có bảng biến thiên như hình vẽ bên.
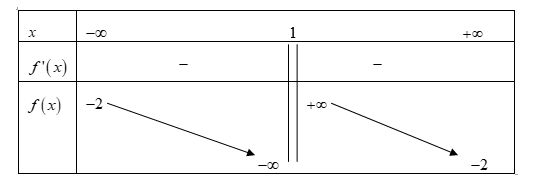
Giá trị a + c thuộc khoảng nào dưới đây?
