Diện tích hình phẳng giới hạn bởi parabol y=x2+x−2 và đường thẳng y=(m+1)+2 có giá trị nhỏ nhất bằng
A. 11
B. 212.
C. 323.
D. 232.
Giải bởi Vietjack
Phương trình hoành độ giao điểm của parabol và đường thẳng đã cho là
x2+x−2=(m+1)x+2⇔x2−mx−4=0 (1).
Do phương trình (1) có P = -4 < 0 nên nó luôn có hai nghiệm phân biệt trái dấu. Giả sử hai nghiệm đó là x1,x2(x1<x2). Theo định lí Vi-ét ta có:
{x1+x2=mx1.x2=−4.
Diện tích hình phẳng giới hạn bởi parabol y=x2+x−2 và đường thẳng y=(m+1)x+2 là:
S=x2∫x1|x2+x−2−[(m+1)x+2]|dx=x2∫x1|x2−mx−4|dx=−x2∫x1(x2−mx−4)dx=x1∫x2(x2−mx−4)dx
=(13x3−m2x2−4x)|x1x2=13(x31−x32)−m2(x21−x22)−4(x1−x2)
=16(x1−x2)[2(x21+x1x2+x22)−3m(x1+x2)−24]
=16(x1−x2)[2(x1+x2)2−2x1x2−3m(x1+x2)−24]
=16(x1−x2)(2m2+8−3m2=24)=16(x1−x2)(m2+16).
Suy ra S2=136(x2−x1)2(m2+16)2=136[(x1+x2)2−4x1x2](m2+16)2=136(m2+16)3
⇒S2≥136.163=10249⇒S≥323.
Dấu “=” xảy ra ⇔m=0
Vậy Smin=323 khi m = 0.
Chọn C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):(x−3)2+(y−2)2+(z−1)2=3 có tâm I và đường thẳng d:x−12=y+63=z+22. Gọi A là điểm nằm trên đường thẳng d. Từ A kẻ các tiếp tuyến AB, AC, AD đến mặt cầu (S) với B, C, D là các tiếp điểm. Khi thể tích khối chóp I.BCD đạt giá trị lớn nhất, mặt phẳng (BCD) có phương trình là mx+ny+pz+12=0. Giá trị của m + n + p bằng
Cho F(x) là một nguyên hàm của hàm số f(x) = 4x + cos2x thỏa mãn F(0) = 1. Giá trị F(π) bằng
Trong không gian Oxyz, cho điểm A(0; -1; -6) và đường thẳng d:x−42=y−21=z+11−6. Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến mặt phẳng (P) lớn nhất. Khoảng cách từ điểm M(5; 1; 1) đến mặt phẳng (P) bằng
Trong không gian Oxyz, cho mặt cầu (S):x2+y2+z2−8x+2y+1=0. Tâm của mặt cầu (S) có tọa độ là
Cho hàm số f(x) = sinx - 1. Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số f(x)=ax−2bx+c với a,b,c∈ℝ có bảng biến thiên như hình vẽ bên.
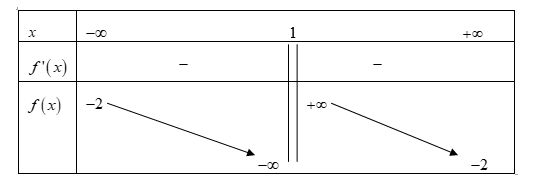
Giá trị a + c thuộc khoảng nào dưới đây?
Thể tích V của khối trụ có chiều cao h = 3cm bán kính r = 2cm bằng
