Cho mặt cầu S(O; 4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S(O; 4) .Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
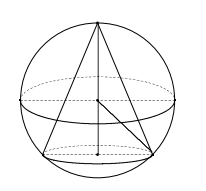
Gọi r, h lần lượt là bán kính đáy và chiều cao của hình nón (N). Dễ thấy lớn nhất thì
Áp dụng định lí Pytago ta có:
Xét hàm số với ta có:
BBT:
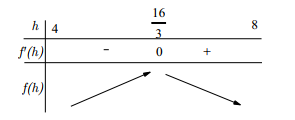
Dựa vào BBT ta thấy
Vậy đặt GTLN khi
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, cho mặt cầu Khi đó (S) có tâm I và bán kính R lần lượt là:
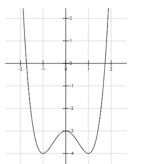
Cho hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
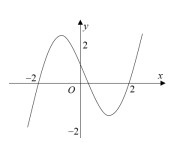
Cho hàm số f(x) có đạo hàm trên là Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 2021] để hàm số đồng biến trên khoảng (0; 2)
Cho khối nón có độ dài đường sinh bằng 2a góc giữa đường sinh và mặt phẳng đáy bằng Thể tích của khối nón đã cho là:
Một ngân hàng X quy định về số tiền nhận được của ngân hàng sau n năm gửi vào ngân hàng tuân theo công thức trong đó A là số tiền gửi ban đầu của khác hàng. Hỏi số tiền ít nhất mà khách hàng B phải gửi vào ngân hàng X là bao nhiêu để sau 5 năm khác hàng đó rút ra được lớn hơn 950 triệu đồng (kết quả làm tròn đến hàng triệu)?
Gọi S là tập hợp các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập S. Tính xác suất để số được chọn có đúng bốn chữ số lẻ và chữ số 0 có hai chữ số kề nó là chữ số lẻ.
Cho hình phẳng D giới hạn bởi các đường và trục hoành. Tính thể tích của khối tròn xoay tạo thành khi quay ![]() quanh trục hoành.
quanh trục hoành.
Trong không gian Oxyz cho điểm M(-4; 2; 3). Tìm tọa độ điểm N đối xứng với M qua Oy
Cho hình chóp S.ABC có và đáy ABC là tam giác đều. Khẳng định nào sau đây sai?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S lên (ABCD) là trung điểm của cạnh AD, đường thẳng SD tạo với đáy một góc bằng Thể tích của khối chóp S.ABCD bằng:
Cho hàm số y = f(x) xác định trên và có đạo hàm Tìm số điểm cực trị của hàm số đã cho?