Có bao nhiêu cặp số nguyên dương (x, y) thỏa mãn lnx+15y+1≤25y4+10y3−x2y2−2y2x, với y≤2022?
Giải bởi Vietjack
Ta có: 25y4+10y3−x2y2−2y2x
=25y4+10y3+y2−x2y2−2y2x−y2
=(25y4+10y3+y2)−(x2y2+2y2x+y2)
=y2(25y2+10y+1)−y2(x2+2x+1)
=y2[(5y+1)2−(x+1)2]
Do đó: lnx+15y+1≤25y2+10y3−x2y2−2y2x
⇒ln(x+1)−ln(5y+1)≤y2[(5y+1)2−(x+1)2]
+) TH1: x+1>5y+1 thì vế phải âm (không thỏa mãn).
+) TH2: x+1≤5y+1 thì vế trái không dương, vế phải không âm nên sẽ luôn thỏa mãn khi
{[{x+1>05y+1>0{x+1<05y+1<0x+1≤5y+1⇔{[{x>−1y>−15{x<−1y<−15x≤5y. Do x, y là số nguyên dương nên ta có:
{{x>−1y>−15x≤5y⇔{x≥1y≥1x≤5y(y≤2022;x,y∈ℤ).
Vậy y∈[1;2022],x∈[1;10110].
Ứng với mỗi y nguyên dương có 5y cặp (x, y) Do đó số cặp:
5(1+2+3+...+2022)=5.2022.20232=10226265 cặp.
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Công thức tính thể tích V của khối trụ có bán kính đáy r và chiều cao h là
Chọn ngẫu nhiên một số trong 17 số nguyên dương đầu tiên. Xác suất để chọn được số nguyên tố bằng
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y=1−4x2x−1?
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, tam giác ABD đều cạnh bằng a√2,SA=3a√22 và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SO và mặt phẳng (ABCD) bằng
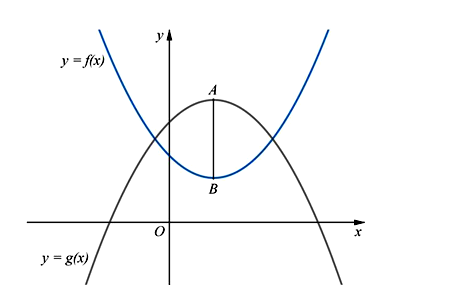
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là các đường cong như hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là B, đồ thị hàm số y = g(x) có đúng một điểm cực trị là A và AB=74. Có bao nhiêu số nguyên m∈(−2021;2021) để hàm số y=||f(x)−g(x)|+m| có đúng 5 điểm cực trị?
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là
